1. \[n^{3}\] is odd. Which of the following statements is/are true?
I. n is odd
II. \[n^{2}\] is odd
III. \[n^{2}\] is even
a) I only
b) II only
c) I and II only
d) I and III only
Explanation: If n3 is odd then n and n2 will also be odd.
2. \[\left(BE\right)^{2}\] = MPB, where B, E, M and P are distinct integers, then M = ?
a) 2
b) 3
c) 9
d) None of these
Explanation: (BE)2 = MPB
If LHS has square, then according to question unit’s digit of RHS can be 0, 1, 4, 5, 6, 9
If B = 0, then (BE)2 cannot be a three digit number
If B \[\neq\] 1 then LHS exceeds 3 digits and is not compatible with RHS.
So B = 1
E = 1 or 9
1 is rejected since B & E are distinct integers
hence BE = 19
M = 3
3. Three wheels can complete respectively 60,36,24 revolutions per minute. There is a red spot on each wheel that touches the
ground at time zero. After how much time, all these spots will simultaneously touch the ground again?
a) 5/2 seconds
b) 5/3 seconds
c) 5 seconds
d) 7.5 seconds
Explanation:

4. A certain number when divided by 899 leaves the remainder 63. Find the remainder when the same number is divided by 29.
a) 5
b) 4
c) 1
d) Cannot be determined
Explanation: Dividend = Divisor × Quotient + Remainder
= 899 Q + 63
Dividend = 29 × 31Q + 29 × 2 + 5
= 29(31Q + 2) + 5
Hence, remainder = 5 when same no. is divided by 29
5. A is the set of positive integers such that when divided by 2,3,4,5 and 6 leaves the remainders 1,2,3,4 and 5 respectively. How
many integer(s) between 0 and 100 belongs to set A?
a) 0
b) 1
c) 2
d) None of these
Explanation: Note that, 2 - 1 = 3 - 2 = 4 - 3 = 5 - 4 = 6 - 5 = 1
Hence, the required number will be of the form LCM of (2, 3, 4, 5, 6) n – 1 where n is any integer
LCM of 2, 3, 4, 5, 6 is 60. Hence the elements of A will be of the form 60n – 1, where n is any integer.
Only for n is equal to 1 the number (60 – 1= 59) will be between 0 and 100.
Hence, only one integer between 0 and 100 belongs to A
6. Number of students who have opted the subjects A, B, C are 60, 84, 108 respectively. The examination is to be conducted for these
students such that only the students of the same subject are allowed in one room. Also the number of students in each room must
be same. What is the minimum number of rooms that should be arranged to meet all these conditions?
a) 28
b) 60
c) 12
d) 21
Explanation:

7. What is the digit in the unit place of \[2^{51}\] ?
a) 2
b) 8
c) 1
d) 4
Explanation:

8. A hundred digit number is formed by writing first 54 natural numbers in front of each other as 12345678910111213.................5354.
Find the remainder when this number is divided by 8
a) 4
b) 7
c) 2
d) 0
Explanation: Given number = (1234...51525)×1000 + 354
Since 1000 = 8 × 125
So, remainder when 354 divided by 8 be 2
Required remainder = 2
9. If n = 1 + x, where ‘x’ is the product of four consecutive positive integers, then which of the following statements is/are true?
I. ‘n’ is odd
II. ‘n’ is prime
III. ‘n’ is perfect square
a) I only
b) II only
c) III only
d) I & III only
Explanation:
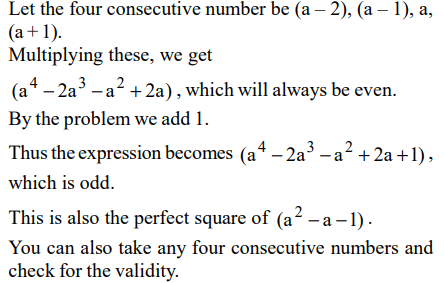
10. \[n^{2}\] = 12345678987654321, then n = ?
a) 1246789
b) 12345321
c) 1111111
d) 11111111
Explanation: Square root of given number = 11111111