1. A graph may be defined as a set of points connected by lines called edges. Every edge connects a pair of points. Thus, a triangle
is a graph with 3 edges and 3 points. The degree of a point is the number of edges connected to it. For example, a triangle is a
graph with three points of degree 2 each. Consider a graph with 12 points. It is possible to reach any point from any other point
through a sequence of edges. The number of edges, e, in the graph must satisfy the condition
a) \[11\leq e\leq 66\]
b) \[10\leq e\leq 66\]
c) \[11\leq e\leq 65\]
d) \[0\leq e\leq 11\]
Explanation: There are 12 points. Since they can be reached from any other point, the edges will be \[^{12}C_{2}\] = 66. Also the minimum number of edges will be 11.
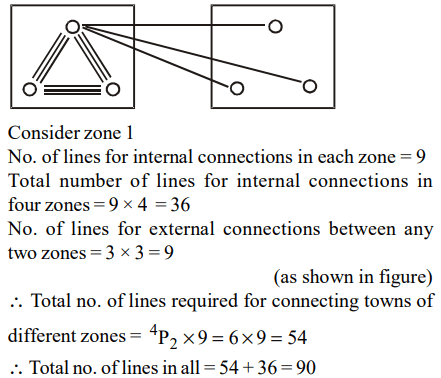
2. There are 12 towns grouped into four zones with three towns per zone. It is intended to connect the towns with telephone lines
such that every two towns are connected with three direct lines if they belong to the same zone, and with only one direct line
otherwise. How many direct telephone lines are required?
a) 72
b) 90
c) 96
d) 144
Explanation:
3. An intelligence agency forms a code of two distinct digits selected from 0, 1, 2, ............ , 9 such that the first digit of the code is
nonzero. The code, handwritten on a slip, can however potentially create confusion when read upside down –– for example, the
code 91 may appear as 16. How many codes are there for which no such confusion can arise?
a) 80
b) 78
c) 71
d) 69
Explanation:

4. N persons stand on the circumference of a circle at distinct points. Each possible pair of persons, not standing next to each other,
sings a two-minute song one pair after the other. If the total time taken for singing is 28 minutes, what is N?
a) 5
b) 7
c) 9
d) None of these
Explanation: There are 28 minutes, hence total no. of songs are 14. Since each pair sings one song. Hence, total number of pairs is 14.
Since, in each possible pair persons are not standing next to each other.
\[^{n}C_{2}\] - n = 14
n = 7
Hence, total number of people = 7.
5. Suppose n is an integer such that the sum of the digits of n is 2, and 1010 < n < 1011. The number of different values for n is
a) 11
b) 10
c) 9
d) 8
Explanation: As 1010 < n < 1011, it means that n has 11 digits. Further sum of digits of n = 2, it means that either there are 2 one’s or a ‘two’ in the whole digit, 2 one’s can be obtained by fixing the first digit as 1 and the remaining 10 digits can be organised in 10 ways.
In case of one ‘2’ there can be only 1 possibility with 2 as the 1st digit.
Hence, total no. of different values for n = 10 + 1 = 11
6.Each family in a locality has at most two adults, and no family has fewer than 3 children. Considering all the families together, there
are more adults than boys, more boys than girls, and more girls than families. Then the minimum possible number of families in
the locality is
a) 4
b) 5
c) 2
d) 3
Explanation: Given that A > B > G > F. Satisfying this condition, if F = 2, then, G = 3, B = 4, A = 5.
But this violates the condition that adults per family should be atmost 2. Hence, we take the next option : F = 3, then G = 4, B = 5, A = 6.
Here all conditions are satisfied. Hence, the answer is (d).
7. In the adjoining figure, the lines represent one-way roads allowing travel only northwards or only westwards. Along how many
distinct routes can a car reach point B from point A?
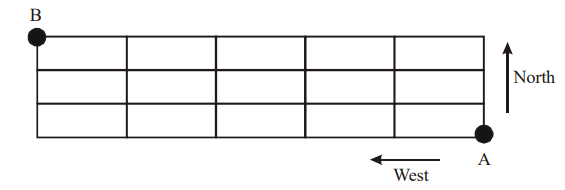
a) 15
b) 56
c) 120
d) 336
Explanation:

8. A new flag is to be designed with six vertical stripes using some or all of the colours yellow, green, blue and red. Then, the number
of ways this can be done such that no two adjacent stripes have the same colour out is
a) 12 × 81
b) 16 × 125
c) 20 × 125
d) 24 × 216
Explanation: There are 6 stripes. The first stripe can be coloured in 4 ways, 2nd in 3, 3rd in 3, and so on. Thus total no. of ways = 4 × 3 × 3 × 3 × 3 × 3 = 12 × 81.
9. In a chess competition involving some boys and girls of a school, every student had to play exactly one game with every other
student. It was found that in 45 games both the players were girls and in 190 games both were boys. The number of games in
which one player was a boy and the other was a girl is
a) 200
b) 216
c) 235
d) 256
Explanation:
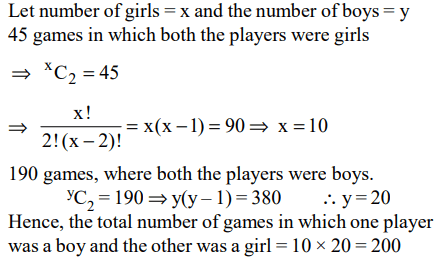
10. Three Englishmen and three Frenchmen work for the same company. Each of them knows a secret not known to others. They
need to exchange these secrets over person-to-person phone calls so that eventually each person knows all six secrets. None of
the Frenchmen knows English, and only one Englishman knows French. What is the minimum number of phone calls needed for
the above purpose?
a) 5
b) 10
c) 9
d) 15
Explanation:
