1. There are 10 points on a line and 11 points on another line, which are parallel to each other. How many triangles can be drawn
taking the vertices on any of the line?
a) 1,050
b) 2,550
c) 150
d) 1,045
Explanation:

2. There are three boxes with 2 red, 2 white and one red and one white ball. All of them are mislabelled. You have to correct all the
labels by picking only one ball from any one of the boxes. Which is the box that you would like to open
a) White
b) Red
c) Red & White
d) None of these
Explanation: Since all are mislabeled open red / white. Now,
if red comes out then both are red in the box. And now change the label, make the box as all red. Now change all white in red / white and all red into all white. Labels are now correct.
If white comes out then both are white in the box. And now change the label, make the box as all white. Now change all red in red / white and all white into all red. Labels are now correct.
3. Out of 2n+1 students, n students have to be given the scholarships. The number of ways in which at least one student can be
given the scholarship is 63. What is the number of students receiving the scholarship?
a) 5
b) 7
c) 3
d) 9
Explanation:
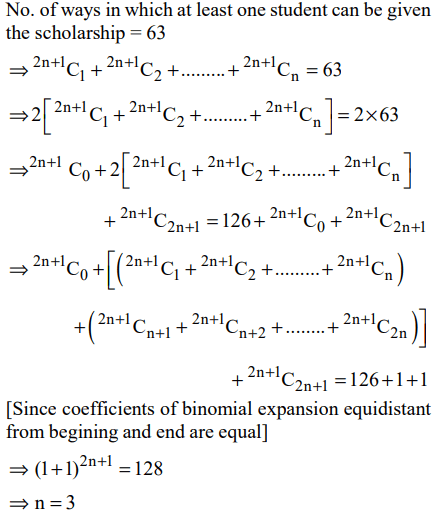
4. Sameer has to make a telephone call to his friend Harish Unfortunately he does not remember the 7- digit phone number. But he
remembers that the first 3 digits are 635 or 674, the number is odd and there is exactly one 9 in the number. The minimum number
of trials that Sameer has to make to be successful is
a) 10,000
b) 3,402
c) 32,00
d) 5,000
Explanation: There are two ways of selecting 635 or 674. If last digit is 9 , then there are 9 ways of filling each of the remaining 3 digits.
Thus total no. of this type of numbers = 2 × 93 = 1,458.
When last digit is not 9, total no. of this type of numbers = 2 × 3 × 4 × 92 = 1944.
[9 can be selected at any of the 4th, 5th or 6th place in 3 ways. Also at the unit place 4 odd nos. except 9 can be used.]
Thus required no. = 1,944 + 1,458 = 3,402
5. There are three books on table A which has to be moved to table B. The order of the book on Table A was 1, 2, 3, with book 1 at
the bottom. The order of the book on table B should be with book 2 on top and book 1 on bottom. Note that you can pick up the
books in the order they have been arranged. You can’t remove the books from the middle of the stack. In how many minimum
steps can we place the books on table B in the required order?
a) 1
b) 2
c) 3
d) 4
Explanation: First step — take book 3 to the table B and, second step — put the book 2 on top of 3. Third step — Transfer the arrangement and keep it over book 1 on table A. The last step is transfer the whole arrangement to the table B which is the fourth step to take. Thus total 4 steps are required
6. X is an odd integer such that 100 < x < 200 and x is divisible by 3 but not 7. The possible number of values of x is
a) 16
b) 15
c) 14
d) 13
Explanation: Between 100 and 200 no.of multiple of 3 are 102 , 105........,198 these when are counted
We find 33 such numbers And out of these 16 are odd.
But 105, 126, 147, 168, 189 are multiple of 21.
And three of these are odd.
Thus required no. = 16 – 3 = 13
7. One red, three white and two blue flags are to be arranged in such a way that no two flags of the same colour are adjacent and the
flags at the two ends are of different colours. The number of ways in which this can be done is
a) 6
b) 8
c) 4
d) 12
Explanation: There are three white flags and ends having different colours, the only possibility at the ends are red and white or white and blue.
W___W___W___ the empty spaces can be filled in 3 ways by one red and two blue flags.
___W___W___W again the empty spaces can be filled in 3 ways so, the total number of ways will be 6
8. There are five boxes each of a different weight and none weighing more than 100. Arun weights two boxes at a time and obtains
the following readings in grams : 110, 112, 113, 114, 116, 117, 118, 119, 120, 121. What is the weight of the heaviest box?
a) 60
b) 61
c) 64
d) can't be determined
Explanation:
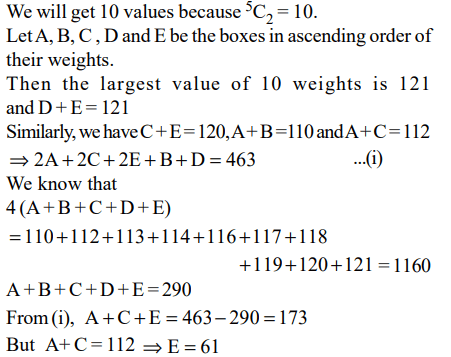
9.A red light flashes 3 times per minute and a green light flashes 5 times in two minutes at regular intervals. If both lights start
flashing at the time, how many times do they flash together in each hour?
a) 30
b) 24
c) 20
d) 60
Explanation: Red light flashes 3 times / min. i.e after every 20 seconds.
Green light flashes 5 times in 2 min. i.e. after every 24 seconds.
So, they flash together after every 2 minutes = 120 seconds
(L.C.M. of 20 & 24 = 120)
Hence, in 1 hour they flash together 60/2 = 30 times
10. Ashish is given Rs. 158 in one rupee denominations. He has been asked to allocate them into a number of bags such that any
amount required between Re. 1 and Rs. 158 can be given by handing out a certain number of bags without opening them. What
is the minimum number of bags required?
a) 11
b) 12
c) 13
d) None of these
Explanation: Minimum number of bags we have to allocate them in such a way that we get all the numbers
i.e., 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128
Hence, minimum no. of bags required is 8; having number of coins 20, 21, 22 ,...., 27