1. Five bells begin to toll together and toll respectively at intervals of 6, 5, 7, 10 and 12 seconds. How many times will they toll together in one hour excluding the one at the start ?
a) 7 times
b) 8 times
c) 9 times
d) 11 times
Explanation: L.C.M. of 6, 5, 7, 10 and 12 is 420.
So, the bells will toll together after every 420 seconds i.e. 7 minutes.
Now, 7 x 8 = 56 and 7 x 9 = 63.
Thus, in 1-hour (or 60 minutes), the bells will toll together 8 times, excluding the one at the start.
2. A bus starts from city X. The number of women in the bus is half of the number of men. In city Y, 10 men leave the bus and five women enter. Now, number of men and women is equal. In the beginning, how many passengers entered the bus ?
a) 15
b) 30
c) 36
d) 45
Explanation: Originally, let number of women = x. Then, number of men = 2x.
So, in city Y, we have : (2x - 10) = (x + 5) or x - 15.
Therefore Total number of passengers in the beginning = (x + 2x) = 3x = 45.
3. A, B, C, D and E play a game of cards. A says to B, "If you give me 3 cards, you will have as many as I have at this moment while if D takes 5 cards from you, he will have as many as E has." A and C together have twice as many cards as E has. B and D together also have the same number of cards as A and C taken together. If together they have 150 cards, how many cards has C got
a) 28
b) 29
c) 31
d) 35
Explanation: Clearly, we have :
A = B - 3 ...(i)
D + 5 = E ...(ii)
A+C = 2E ...(iii)
B + D = A+C = 2E ...(iv)
A+B + C + D + E=150 ...(v)
From (iii), (iv) and (v), we get: 5E = 150 or E = 30.
Putting E = 30 in (ii), we get: D = 25.
Putting E = 30 and D = 25 in (iv), we get: B = 35.
Putting B = 35 in (i), we get: A = 32.
Putting A = 32 and E = 30 in (iii), we get: C = 28.
4. A farmer built a fence around his square plot. He used 27 fence poles on each side of the square. How many poles did he need altogether ?
a) 100
b) 104
c) 108
d) None of these
Explanation: Since each pole at the corner of the plot is common to its two sides, so we have :
Total number of poles needed = 27 x 4 - 4 = 108 - 4 = 104.
5. In a city, 40% of the adults are illiterate while 85% of the children are literate. If the ratio of the adults to that of the children is 2 : 3, then what percent of the population is literate ?
a) 20%
b) 25%
c) 50%
d) 75%
Explanation:

6. The number of boys in a class is three times the number of girls. Which one of the following numbers cannot represent the total number of children in the class ?
a) 48
b) 44
c) 42
d) 40
Explanation: Let number of girls = x and number of boys = 3x.
Then, 3x + x = 4x = total number of students.
Thus, to find exact value of x, the total number of students must be divisible by 4.
7. A shepherd had 17 sheep. All but nine died. How many was he left with ?
a) Nil
b) 8
c) 9
d) 17
Explanation: 'All but nine died' means 'All except nine died' i.e. 9 sheep remained alive
8. In a family, the father took 1/4 of the cake and he had 3 times as much as each of the other members had. The total number of family members is
a) 3
b) 7
c) 10
d) 12
Explanation:
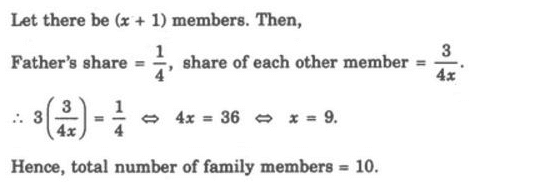
9. In three coloured boxes - Red, Green and Blue, 108 balls are placed. There are twice as many balls in the green and red boxes combined as there are in the blue box and twice as many in the blue box as there are in the red box. How many balls are there in the green box ?
a) 18
b) 36
c) 45
d) None of these
Explanation: Let R, G and B represent the number of balls in red, green and blue boxes respectively.
Then, .
R + G + B = 108 ...(i),
G + R = 2B ...(ii)
B = 2R ...(iii)
From (ii) and (iii), we have G + R = 2x 2R = 4R or G = 3R.
Putting G = 3R and B = 2R in (i), we get:
R + 3R + 2R = 108 ⇔ 6R = 108 ⇔ R = 18.
Therefore Number of balls in green box = G = 3R = (3 x 18) = 54.
10. In a cricket match, five batsmen A, B, C, D and E scored an average of 36 runs. D Scored 5 more than E; E scored 8 fewer than A; B scored as many as D and E combined; and B and C scored 107 between them. How many runs did E score ?
a) 62
b) 45
c) 28
d) 20
Explanation: otal runs scored = (36 x 5) = 180.
Let the runs scored by E be x.
Then, runs scored by D = x + 5; runs scored by A = x + 8;
runs scored by B = x + x + 5 = 2x + 5;
runs scored by C = (107 - B) = 107 - (2x + 5) = 102 - 2x.
So, total runs = (x + 8) + (2x + 5) + (102 - 2x) + (x + 5) + x = 3x + 120.
Therefore 3x + 120 =180 ⇔ 3X = 60 ⇔ x = 20.