1.One pipe can fill a tank three times as fast as another pipe. If together the two pipes can fill the tank in 36 minutes, then the slower pipe alone will be able to fill the tank in:
a) 81 minutes
b) 108 minutes
c) 144 minutes
d) 192 minutes
Explanation:
$$\eqalign{ & \frac{1}{x} + \frac{3}{x} = \frac{1}{{36}} \cr & \frac{4}{x} = \frac{1}{{36}} \cr & x = 144\,\text{minutes} \cr} $$
2. A large tanker can be filled by two pipes A and B in 60 minutes and 40 minutes respectively. How many minutes will it take to fill the tanker from empty state if B is used for half the time and A and B fill it together for the other half?
a) 15 minutes
b) 20 minutes
c) 27.5 minutes
d) 30 minutes
Explanation:
$$\eqalign{ & {\text{Part}}\,{\text{filled}}\,{\text{by}}\,(A + B)\,{\text{in}}\,{\text{1}}\,{\text{minute}} \cr & = {\frac{1}{{60}} + \frac{1}{{40}}} = \frac{1}{{24}} \cr & {\text{Suppose}}\,{\text{the}}\,{\text{tank}}\,{\text{is}}\,{\text{filled}}\,{\text{in}}\,x\,{\text{minutes}} \cr & {\text{Then}},\,\frac{x}{2}\left( {\frac{1}{{24}} + \frac{1}{{40}}} \right) = 1 \cr & \frac{x}{2} \times \frac{1}{{15}} = 1 \cr & x = 30\,\text{minutes} \cr} $$
3. A tap can fill a tank in 6 hours. After half the tank is filled, three more similar taps are opened. What is the total time taken to fill the tank completely?
a) 3 hrs 15 min
b) 3 hrs 45 min
c) 4 hrs
d) 4 hrs 15 min
Explanation: Time taken by one tap to fill half of the the tank = 3 hours
Part filled by the four taps in 1 hour
$$\eqalign{ & = {4 \times \frac{1}{6}} = \frac{2}{3} \cr & {\text{Remaining}}\,{\text{part}} = {1 - \frac{1}{2}} = \frac{1}{2} \cr & \frac{2}{3}:\frac{1}{2}::1:x \cr & \Rightarrow x = {\frac{1}{2} \times 1 \times \frac{3}{2}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{3}{4}\,hrs.\,\,i.e.,\,45\,\operatorname{mins} . \cr & {\text{So,}}\,{\text{total}}\,{\text{time}}\,{\text{taken}} = 3\,hrs.\,45\,mins. \cr} $$
4.Three taps A, B and C can fill a tank in 12, 15 and 20 hours respectively. If A is open all the time and B and C are open for one hour each alternately, the tank will be full in:
a) 6 hours
b) $$6\frac{2}{3}$$ hours
c) 7 hours
d) $$7\frac{1}{2}$$ hours
Explanation:
$$\eqalign{ & \left( {{\text{A + B}}} \right){\text{'s 1 hour work}} \cr & {\text{ = }} {\frac{1}{{12}} + \frac{1}{{15}}} = \frac{9}{{60}} = \frac{3}{{20}} \cr & \left( {{\text{A + C}}} \right){\text{'s 1 hour work}} \cr & {\text{ = }} {\frac{1}{{12}} + \frac{1}{{20}}} = \frac{8}{{60}} = \frac{2}{{15}} \cr & {\text{Part filled in 2 hrs}} \cr & {\text{ = }} {\frac{3}{{20}} + \frac{2}{{15}}} = \frac{{17}}{{60}} \cr & {\text{Part filled in 6 hrs}} \cr & {\text{ = }} {3 \times \frac{{17}}{{60}}} = \frac{{17}}{{20}} \cr & {\text{Remaining part}} \cr & {\text{ = }} {1 - \frac{{17}}{{20}}} = \frac{3}{{20}} \cr} $$
Now it is the turn of A and B and
$$\frac{3}{{20}}$$ part is filled by A and B in 1 hour
Total time taken to fill tank
= (6 + 1) hrs
= 7 hrs
5. Three pipes A, B and C can fill a tank in 6 hours. After working at it together for 2 hours, C is closed and A and B can fill the remaining part in 7 hours. The number of hours taken by C alone to fill the tank is:
a) 10
b) 12
c) 14
d) 16
Explanation: Part filled in 2 hours = $$\frac{2}{6}$$ = $$\frac{1}{3}$$
Remaining part = $$ {1 - \frac{1}{3}} $$ = $$\frac{2}{3}$$
(A + B)'s 7 hour's work = $$\frac{2}{3}$$
(A + B)'s 1 hour's work = $$\frac{2}{{21}}$$
C's 1 hour's work = {(A + B + C)'s 1 hour's work} - {(A + B's 1 hour's work}
$$\eqalign{ & = {\frac{1}{6} - \frac{2}{{21}}} \cr & = \frac{1}{{14}} \cr} $$
C alone can fill the tank in 14 hours
6. Three taps A, B, C can fill an overhead tank in 4, 6 and 12 hours respectively. How long would the three taps take to fill the tank if all of them are opened together ?
a) 2 hours
b) 4 hours
c) 3 hours
d) 5 hours
Explanation:
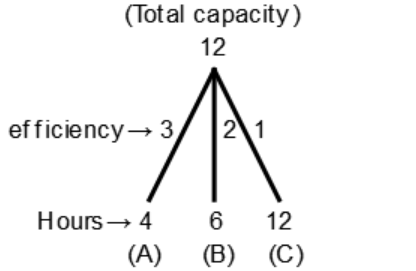
(A + B + C)'s efficiency
= 3 + 2 + 1
= 6 units/hr
(A + B + C) can fill the tank in
$$\eqalign{ & {\text{ = }}\frac{{{\text{Total Capacity}}}}{{{\text{Efficiency of}}\left( {{\text{A + B + C}}} \right){\text{ }}}} \cr & = \frac{{12}}{6} \cr & = 2{\text{ hours}} \cr} $$
7. Having the same capacity 9 taps fill up a water tank in 20 minutes. How many taps of the same capacity are required to fill up the same water tank in 15 minutes ?
a) 10 taps
b) 12 taps
c) 15 taps
d) 18 taps
Explanation:
$$\eqalign{ & \left[ {\frac{{{m_1} \times {h_1} \times {t_1}}}{{{w_1}}} = \frac{{{m_2} \times {h_2} \times {t_2}}}{{{w_2}}}} \right] \cr & {9_{taps}} \times {20_{\min }} = {t_{taps}} \times {15_{\min }} \cr & t = 12\,\,{\text{taps}} \cr} $$
8. Pipe A can fill a tank in 4 hours and pipe B can fill it 6 hours. If they are opened on alternate hours and if pipe A is opened first then in how many hours, the tank shall be full ?
a) $${\text{4}}\frac{1}{2}$$ hours
b) $${\text{4}}\frac{2}{3}$$ hours
c) $${\text{3}}\frac{1}{2}$$ hours
d) $${\text{3}}\frac{1}{4}$$ hours
Explanation: A → 4 hours
B → 6 hours

⇒ For the first hour tap A is opened and B for second hour
⇒ Work done by both in 2 hours
$$\eqalign{ & \to \left( {3\,{\text{lit/h}} + 2\,{\text{lit/h}}} \right) \times 2 = 10\,{\text{units}} \cr & \,\,\,\,\,\,\,\,\mathop {\,\,|\,\,\, \times 2}\limits_{{\text{4 hours}}}^{{\text{2 hours}}} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathop {\,\,|\,\,\, \times 2}\limits_{{\text{10 litres}}}^{{\text{5 liters}}\,} \cr} $$
⇒ Remaining part
= 12 - 10 = 2 liters
⇒ Again 5th hour A will be opened Tap A will fill the 2 liters water with its efficiency = $$\frac{2}{3}$$ hours
Therefore tank will be filled in
= $$\left( {4 + \frac{2}{3}} \right)$$ hours
= $${\text{4}}\frac{2}{3}$$ hours
9. Pipe A can fill the tank in 8 hours and pipe B can fill it in 12 hours. If pipe A is opened at 7:00 AM and pipe B is opened at 9:00 AM, then at what time will the tank be full ?
a) 12:00 PM
b) 12:30 PM
c) 11:48 PM
d) 12:36 PM
Explanation:
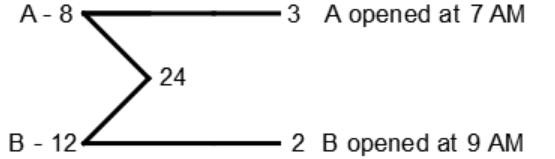
A opened 2 hours early to B
In 2 hours A can do 3 × 2 = 6 unit work
Remaining work = 24 - 6 = 18
A + B can do it in
$$\eqalign{ & = \frac{{18}}{5}{\text{hours}} \cr & = 3\frac{3}{5}{\text{hours}} \cr & {\text{ = 3}}\,{\text{hours 36 minutes}} \cr} $$
Tank will be full in 9 AM + 3 hours 36 minutes = 12.36 PM.
10. Two pipes A and B can fill a tank with water in 30 minutes and 45 minutes respectively. The third pipe C can empty the tank in 36 minutes. First A and B are opened. After 12 minutes C is opened. Total time ( in minutes ) in which the tank will be filled up is -
a) 12 minutes
b) 24 minutes
c) 30 minutes
d) 36 minutes
Explanation:
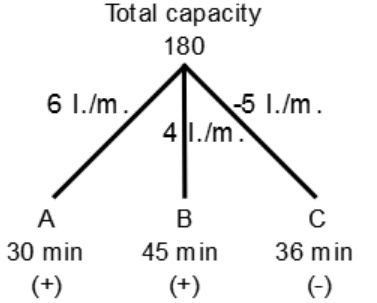
A . . . . . (+) 30 minutes
B . . . . . (+) 45 minutes
C . . . . . (-) 36 minutes
⇒ Water filled by (A + B) in 12 min
= 12 × (6 + 4)
= 12 × 10 = 120 liters
⇒ Remaining capacity
= 180 - 120 = 60 liters
⇒ After 12 minutes emptied pipe C is also opened
⇒ Total capacity (A + B - C)
= (6 + 4 - 5) = 5 liters/minutes
⇒ Time taken by (A + B - C) with capacity 5 liters/minutes to fill the remaining part
$$ = \frac{{60\,\,{\text{liters}}}}{{5\,\,{\text{liters/minutes}}}}{\text{ = 12 minutes}}$$
⇒ Therefore, total time in which the tank will be filled up is
= 12 + 12
= 24 minutes