1.What is multiplication law?
a) A.B =B.A
b) a(A.B) = A.(aB)
c) A.(B+D) = (A.B) + (A.D)
d) a(A.B) = AxB
Explanation: For three vectors A, B and D the various laws are. Communitive law: A.B =B.A. While distributive law is A.(B+D) = (A.B) + (A.D). And multiplication law is a(A.B) = A.(aB).
2. Which is true for two vector A = A1i + A2j + A3k and B = B1i + B2j + B3k?
a) A.B = A1B1 + A2B2 + A3B3
b) AxB = A1B1 + A2B2 + A3B3
c) A.B = A1B2 + A2B3 + A3B1
d) AxB = A1B2 + A2B3 + A3B1
Explanation: The multiplication of x, y and z components with their respective same component give a scalar, equal to 1, i.e. i.i = 1 and j.j = 1, while jxj =0. This is the basic principle of the vector algebra which needs to apply wherever needed
3. Determine the magnitude of the force F = 300j parallel to the direction of AB?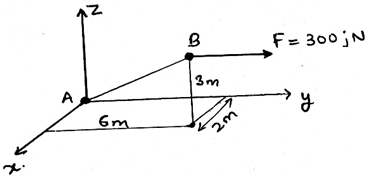
a) 155N
b) 257.1N
c) 200N
d) 175N
Explanation: Force component in the direction parallel to the AB is given by unit vector 0.286i + 0.857j + 0.429k. Now (300j).(0.286i + 0.857j + 0.429k) = 257.1N. Just try to resolve the force into it’s particular components.
4. What is k.i?
a) 0
b) 1
c) -1
d) ∞
Explanation: As the dot product of only the same Cartesian component is unity, i.e. i.i = 1 and j.j =1, rest all remaining dot product will give 0(i.j = 0 and j.k = 0). Cross product of the same plane vectors always gives zero. And dot product of the same plane vector gives a scalar quantity.
5. What is {(i.i) + (-i.j) + (-k.k) + (k.i)}.(Ai +Bj + Cz)?
a) 1
b) 0
c) A + B + C
d) -1
Explanation: {(i.i) + (-i.j) + (-k.k) + (k.i)} = 0. As (1 + 0 + 0 – 1). Cross product of the same plane vectors always give zero. And dot product of the same plane vector gives a scalar quantity
6. α = cos-1(A.B/AB). What is the range of α?
a) 0˚<α<90˚
b) 0˚<α<180˚
c) 90˚<α<180C
d) 0˚<α<45˚
Explanation: Cosine inverse function is defined only between 0˚ to 180˚. It cannot be defined under any of the given range, because this is the principle range of the inverse cosine function.
7. What is the value of {(AxB).(C.D)x(AxB).(C.D)}? For the four vectors A, B, C and D, with A, B, C and D all lying in the same plane?
a) i + j + k
b) √3(i + j + k)
c) 0
d) -1(i + j + k)
Explanation: Here we are trying to do the cross product of the two vectors in the same plane. Which will give us zero. While dot product of the same plane vector will give a scalar quantity, not zero.
8. What is (AxB).(BxA); or A = A1i + A2j + A3k and B = B1i + B2j + B3k?
a) 0
b) A1B1A2B2i + A2B2A3B3j + A3B3A1B1k
c) A1B1A1B2i + A2B2A3B2j + A3B3A1B3k
d) A1B1A2B1i + A2B2A2B3j + A3B3A2B1k
Explanation: Here we are trying to do the cross product of the two vectors in the same plane. Which will give us zero. While dot product of the same plane vector will give a scalar quantity, not zero.
9. What is the dot product of two vectors which are having a magnitude equal to unity and are making an angle of 45°?
a) 0.707
b) -0.707
c) 1.414
d) -1.414
Explanation: The dot product of two vectors having the angle between them equal to 45° will have the product of the vector’s magnitude. As the vectors are of unit magnitude, their product will be unity. Thus the magnitude factor would be cosine function at 45 °.
10. Mathematically, for two vectors A and B of any magnitude, the cross product of both, i.e. AxB = given by:
a) |A||B|sinØ
b) |A||B|
c) |A||B|cosØ
d) |A||B|sin(180°+Ø)
Explanation: The cross product of two vectors gives a vector which is perpendicular to both of the vectors. And the mathematic equation for the same is given by |A||B|sinØ. And the dot product of the same by any of the other two vectors will give the answer zero, as perpendicular