1. Mobility is different than the number of degrees of freedom.
a) True
b) False
Explanation: The mobility or number of degrees of freedom of a rigid body is defined as the number of independent movement the body has. The number of parameters that must be controlled independently to get the device in a particular position is mobility. Mobility and number of degrees of freedom are the same thing.
2. According to Kutzbach criterion, the mobility of a rigid body is given by the formula:
a) 3(n+1)-2j1-j2
b) 3(n+1)+2j1+j2
c) 3(n-1)+2j1+j2
d) 3(n-1)-2j1-j2
Explanation: The Kutzbach criterion is used to determine the number of degree of freedoms of a kinematic chain or a linkage. According to Kutzbach criterion, mobility (m) = 3(n-1)-2j1-j2; where n = number of links, j1 = number of lower pairs, j2 = number of higher pairs.
3. What is the equation for Grubler’s criterion for plane mechanisms with constrained motion?
a) 3n-2j1-4=0
b) 3n-3j1-4=0
c) 3n+2j1+4=0
d) 3n+3j1+4=0
Explanation: Equation for Grubler’s criterion for plane mechanisms with constrained motion can be derived by putting m = 1 and j2 = 0 in the equation of mobility according to Kutzbach criterion.
1 = 3(n-1)-2j1-0
Therefore, 3n-2j1-4=0
4.State the three dimensional form of Kutzbach criterion.
a) 6(n-1)+5j1+4j2+3j3+2j4+j5
b) 6(n-1)-5j1-4j2-3j3-2j4-j5
c) 6(n+1)+5j1+4j2+3j3+2j4+j5
d) 6(n+1)-5j1-4j2-3j3-2j4-j5
Explanation: According to the three dimensional form of Kutzbach criterion, mobility (m) = 6(n-1)-5j1-4j2-3j3-2j4-j5. It is also called as Kutzbach criterion to determine the degree of freedom of a spatial mechanism.
5. Find the mobility of the following three bar mechanism.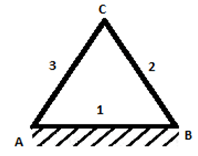
a) 3
b) 2
c) 0
d) 1
Explanation: Here, n = 3, j1 = 3, j2 = 0.
Hence, m = 3(3-1)-(2×3)-0 = 0
As the degree of freedom is 0, there is no relative motion between the links and the mechanism forms a structure.
6. Find the mobility of the given mechanism.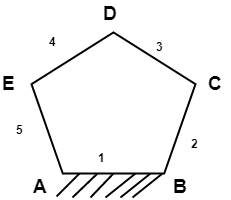
a) 0
b) 1
c) 2
d) 3
Explanation: Here, n = 5, j1 = 5, j2 = 0.
Hence, m = 3(5-1)-(2×5)-0 = 2
As the degree of freedom is 2, two separate input motions are required to produce constrained motion for the mechanism.
7. If there are redundant constraints in the chain and it forms a statically indeterminate structure, what is the degree of freedom or the mobility of this structure?
a) 0
b) 1
c) 2
d) Less than 0
Explanation: If n ≤-1, then there are redundant constraints in the chain and a statically indeterminate structure is formed. The structure is called a preloaded structure as some stress is created within the link so that it has negative mobility.
8. Find the mobility of the given mechanism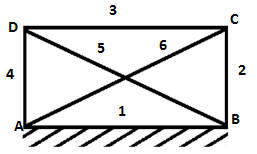
a) -2
b) 2
c) -1
d) 1
Explanation: Here, n = 6, j1 = 8, j2 = 0.
Hence, m = 3(6-1)-(2×8)-0 = -1
The degree of freedom is -1, thus there are redundant constraints in the chain and a statically indeterminate structure is formed
9. Find the mobility of the following mechanism with a higher pair.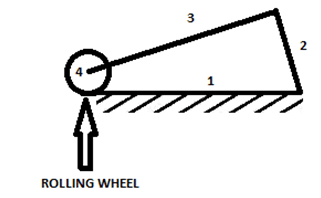
a) 3
b) -1
c) 1
d) 2
Explanation: Here, n = 4, j1 = 3, j2 = 1.
Hence, m = 3(4-1)-(2×3)-1 = 2
The degree of freedom or mobility is 2.
10. State the equation for the three dimensional form of Grubler’s criterion.
a) 6n-5j1-7=0
b) 6n-6j1-6=0
c) 6n+5j1+7=0
d) 6n+6j1+6=0
Explanation: Equation for three dimensional form of Grubler’s criterionfor plane mechanisms with constrained motion can be derived by putting m = 1 and j2= j3 = j4 = j5 = 0 in the equation of mobility according to three dimensional form of Kutzbach criterion.
1 = 6(n-1)-5j1-(4×0)-(3×0)-(2×0)-0
Therefore,6n-5j1-7=0.