1. If the chords of contact of tangents from two points \[\left(x_{1},y_{1}\right)\] and \[\left(x_{2},y_{2}\right)\] to the ellipse \[x^{2}/a^{2}+y^{2}/b^{2}=1\] are
at right angles then \[x_{1}x_{2}/y_{1}y_{2}\] is equal to
a) \[a^{2}/b^{2}\]
b) \[-b^{2}/a^{2}\]
c) \[-a^{4}/b^{4}\]
d) \[-b^{4}/a^{4}\]
Explanation:

2. Let \[E_{1}\] be the ellipse \[\frac{x^{2}}{a^{2}+2}+\frac{y^{2}}{b^{2}}=1\] and \[E_{2}\] be the ellipse \[\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}+1}=1.\] The number of points from
which to perpendicular tangents can be drawn to
each of \[E_{1}\] and \[E_{2}\] is …
a) 0
b) 1
c) 2
d) 4
Explanation:

3.An equation of the ellipse centered at (0,0) having eccentricity
\[\frac{3}{5}\] and passing through (4, 0) is
a) \[16x^{2}+25y^{2}=256\]
b) \[25x^{2}+16y^{2}=400\]
c) \[25x^{2}+16y^{2}=256\]
d) \[16x^{2}+25y^{2}=400\]
Explanation:

4. The number of value of c for which y = 5x + c is a
tangent to the ellipse \[\frac{x^{2}}{25}+y^{2}=1\] is
a) 1
b) 2
c) 4
d) 6
Explanation:

5. If the equation \[\frac{x^{2}}{10-2a}+\frac{y^{2}}{4-2a}=1\] represents an
ellipse, then 'a' lies in the interval
a) \[\left(-\infty ,5\right)\]
b) (2, 5)
c) \[\left(-\infty ,2\right)\]
d) \[\left(5,\infty \right)\]
Explanation:

6. If \[\left(\tan\theta_{1} \right)\left(\tan\theta_{2} \right)=\frac{-a^{2}}{b^{2}},\]
then the chord joining two points \[P_{1}\left(\theta_{1} \right)\] and \[P_{2}\left(\theta_{2} \right)\] on the ellipse \[\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\] will subtend a right angle at
a) focus (ae, 0)
b) focus (–ae, 0)
c) centre (0,0)
d) vertex (a,0))
Explanation:
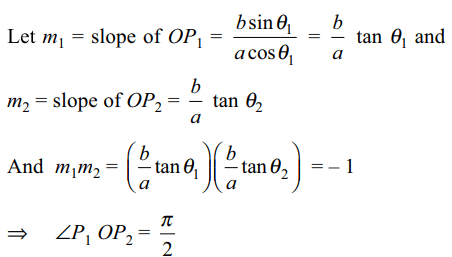
7.Let \[P\left(a \cos\theta ,b\sin\theta\right)\] and \[Q\left(a \cos\phi ,b\sin\phi\right)\] where \[\theta+\phi=\frac{\pi}{2}\]
be two points on the ellipse \[\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\]
The locus of point of intersections of normals at P
and Q is
a) ax + by = 0
b) ax - by = 0
c) x + y = 0
d) x + y = a + b
Explanation:
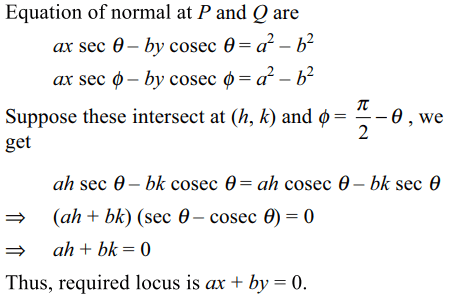
8. The locus of the point of intersection of the tangents at the extremities
of the chord of the ellipse \[x^{2}+2y^{2}=6\] which touches the ellipse \[x^{2}+4y^{2}=4\] is
a) \[x^{2}+y^{2}=6\]
b) \[x^{2}+y^{2}=2\]
c) \[x^{2}+y^{2}=9\]
d)\[x^{2}+y^{2}=12\]
Explanation:
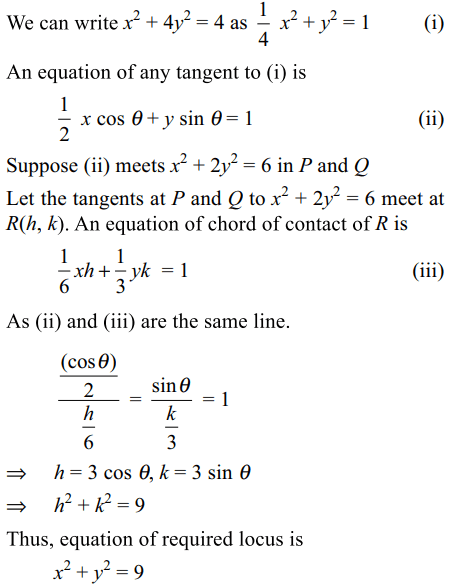
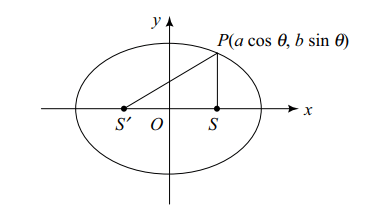
9. If P is a point on the ellipse \[\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=\] with foci S
and S' and eccentricity e, then locus of the incentre
of the triangle PSS' is an ellipse of eccentricity
a) \[\sqrt{\frac{1-e}{1+e}}\]
b) \[\sqrt{\frac{e}{1+e}}\]
c) \[\sqrt{\frac{2e}{1+e}}\]
d) \[\sqrt{\frac{1-2e}{1+e}}\]
Explanation:
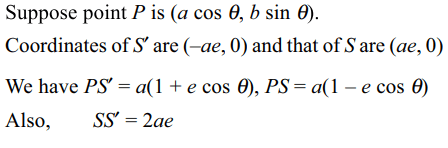
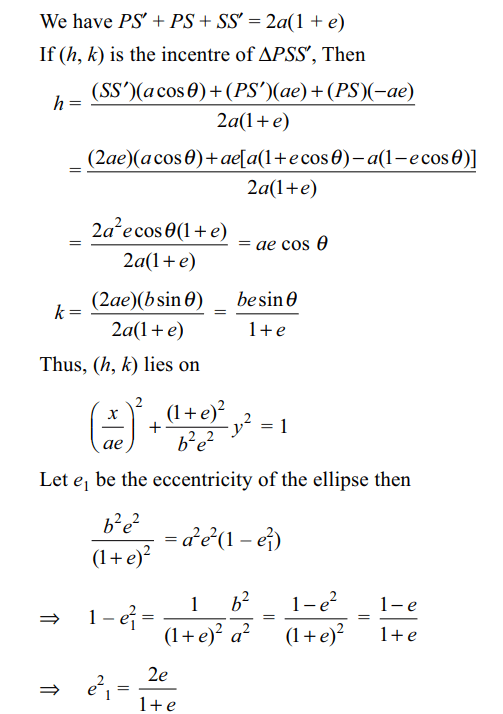
10. Equation of a tangent to the ellipse \[\frac{x^{2}}{25}+\frac{y^{2}}{16}=1\] which cuts off equal intercepts on the axes is
a) \[x+y-\sqrt{41}=0\]
b) \[x-y+\sqrt{41}=0\]
c) x + y – 9 = 0
d) Both a and b
Explanation:
