1. Tree top’s angle of elevation is 30° from a point on ground, 300m away the tree. When the tree grew up its angle of elevation became 60° from the same point. How much did the tree grow?
a) $$100\sqrt 3 \,{\text{m}}$$
b) $${\text{200}}\sqrt 3 \,{\text{m}}$$
c) $$300\frac{1}{{\sqrt 3 }}\,{\text{m}}$$
d) $$\frac{{200}}{{\sqrt 3 }}\,{\text{m}}$$
Explanation:
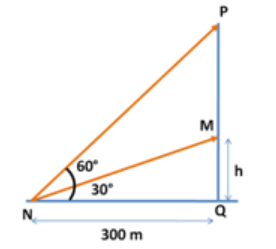
$$\eqalign{ & {\text{Original tree height}} = {\text{h}} = {\text{MQ}} \cr & {\text{New}}\,{\text{tree}}\,{\text{height}} = PQ \cr & {\text{in}}\,\Delta MQN,\,\tan {30^ \circ } = \frac{1}{{\sqrt 3 }} = \frac{{MQ}}{{NQ}} \cr & MQ = \frac{{300}}{{\sqrt 3 }} \cr & {\text{in}}\,\Delta PQN,\,\tan {60^ \circ } = \sqrt 3 = \frac{{PQ}}{{NQ}} \cr & PQ = 300\sqrt 3 \cr & {\text{Tree}}\,{\text{grew}} = PQ - MQ \cr & {\text{Tree}}\,{\text{grew}} = 300\sqrt 3 - \frac{{300}}{{\sqrt 3 }} \cr & = 300\frac{2}{{\sqrt 3 }} \cr & = 3 \times 100 \times \frac{2}{{\sqrt 3 }} \cr & = 200\sqrt 3 \,{\text{m}} \cr} $$
2. TheMohan looks at a tree top and the angle made is 45°. He moves 10 cm back and again looks at the tree top but this time angle made is 30°. How high is the tree top from ground?
a) $$\frac{{10}}{{\sqrt 3 + 1}}\,{\text{cm}}$$
b) $$20\sqrt 3 \,{\text{cm}}$$
c) $$20\,{\text{cm}}$$
d) $$\frac{{10}}{{\sqrt 3 - 1}}\,{\text{cm}}$$
Explanation:
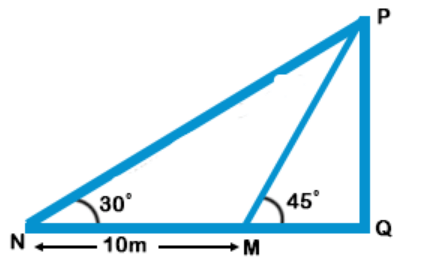
Let PQ be three and M and N be positions where Mphan stands.
$$\eqalign{ & {\text{Now,}}\,{\text{tan}}{45^ \circ } = 1 = \frac{{PQ}}{{MQ}} \cr & PQ = MQ \cr & \tan {30^ \circ } = \frac{1}{{\sqrt 3 }} = \frac{{PQ}}{{NQ}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{PQ}}{{10 + MQ}} \cr & 10 + MQ = \sqrt 3 \,PQ \cr} $$
$$ 10 + PQ = \sqrt 3 \,PQ$$ (As, PQ = MQ)
$$ PQ = \frac{{10}}{{\sqrt 3 - 1}}\,{\text{cm}}$$
3. Rohit while seeing a bird on tree top made 45° angle of elevation. He walks 240ft. towards the tree to observe the bird closely, thus making 60° angle of elevation. How far was Rohit from the tree initially?
a) $$\frac{{240\sqrt 3 }}{{\sqrt 3 - 1}}\,{\text{ft}}$$
b) $$\frac{{240}}{{\sqrt 3 - 1}}\,{\text{ft}}$$
c) $$\frac{{240}}{{\sqrt 3 }}\,{\text{ft}}$$
d) $$240\sqrt 3 \,{\text{ft}}$$
Explanation:
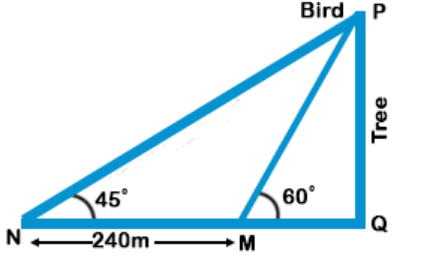
$$\eqalign{ & {\text{Now,}}\,{\text{tan}}{45^ \circ } = 1 = \frac{{PQ}}{{NQ}} \cr & {\text{Tree}}\,{\text{height}} \cr & = PQ = NQ \cr & = \left( {240 + MQ} \right) \cr & \tan {60^ \circ } = \sqrt 3 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{PQ}}{{MQ}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{240 + MQ}}{{MQ}} \cr & 240 + MQ = \sqrt 3 \,MQ \cr & MQ = \frac{{240}}{{\sqrt 3 - 1}}\,{\text{ft}} \cr & NQ = 240 + MQ \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{240\sqrt 3 }}{{\sqrt 3 - 1}}\,{\text{ft}} \cr} $$
= Rohit was this much far away initially
4. A tree breaks and falls to the ground such that its upper part is still partially attached to its stem. At what height did it break, if the original height of the tree was 24 cm and it makes an angle of 30° with the ground?
a) 12 cm
b) 8 cm
c) 9.5 cm
d) 7.5 cm
Explanation: Let the tree break at height h cm from ground at point M.
The broken part makes angle of 30°
Broken Part MP = MN = 24 - h
$$\eqalign{ & {\text{in}}\,\Delta MCQ, \cr & \sin {30^ \circ } = \frac{1}{2} = \frac{{MQ}}{{MN}} = \frac{{\text{h}}}{{24 - {\text{h}}}} \cr & 24 - {\text{h}} = 2{\text{h}} \cr} $$
h = 8 cm = Tree breaks at this height
5. Two houses are in front of each other. Both have chimneys on their top. The line joining the chimneys makes an angle of 45° with the ground. How far are the houses from each other if one house is 25m and other is 10m in height?
a) 18 m
b) 12 m
c) 7.5 m
d) 15 m
Explanation:
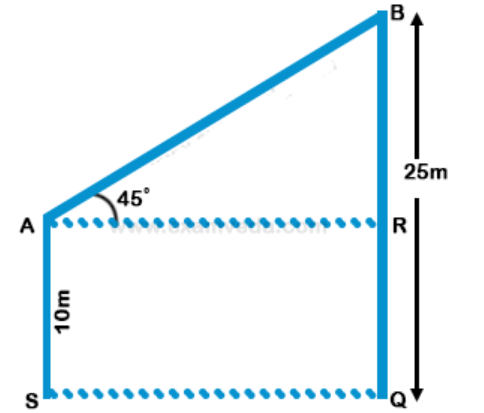
In ∠ABR, ∠ARB = 90° and ∠BAR = 45°
Sum of angles of a triangle = 180°
So ∠ABR = 180 - 90 - 45 = 45°
BR = AR
AS = RQ = 10m
Also, BR = BQ - RQ = 25 - 10 = 15m
AR = 15m = Distance between houses
6. Shadow of a man is $$\frac{1}{{\sqrt 3 }}$$ times the height of the man. What will be the sun’s angle of elevation?
a) 135°
b) 45°
c) 30°
d) 60°
Explanation: Shadow length = $$\frac{1}{{\sqrt 3 }}$$ Height of man
$$\eqalign{ & \frac{{{\text{Height}}\,{\text{of}}\,{\text{man}}}}{{{\text{Shadow}}\,{\text{length}}}} = \sqrt 3 \cr & \tan \theta = \frac{{{\text{Height}}\,{\text{of}}\,{\text{man}}}}{{{\text{Shadow}}\,{\text{length}}}} = \sqrt 3 \cr & {\text{But}}\,\tan {60^ \circ } = \sqrt 3 \cr} $$
$$\theta $$ = 60° = Angle of elevation of sum
7. There is a tree between houses of A and B. If the tree leans on A’s House, the tree top rests on his window which is 12 m from ground. If the tree leans on B’s House, the tree top rests on his window which is 9 m from ground. If the height of the tree is 15 m, what is distance between A’s and B’s house?
a) 21 m
b) 25 m
c) 16 m
d) 12 m
Explanation:
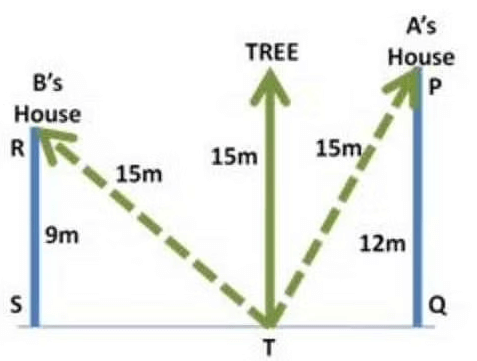
In $$\Delta $$STR, by Pythagoras theorem
$$\eqalign{ & R{T^2} = S{T^2} + R{S^2} \cr & S{T^2} = {15^2} - {9^2} = 144 \cr & ST = 12\,{\text{m}} \cr} $$
In $$\Delta $$TQP, by Pythagoras theorem
$$\eqalign{ & P{T^2} = T{Q^2} + P{Q^2} \cr & T{Q^2} = {15^2} - {12^2} = 81 \cr & TQ = 9\,{\text{m}} \cr} $$
Distance between houses
SQ = ST + TQ
SQ = 12 + 9
SQ = 21 m
8. Ramesh and Suresh’s mud forts have heights 8 cm and 15 cm. They are 24 cm apart. How far are the fort tops from each other?
a) 31 cm
b) 24cm
c) 25 cm
d) 24.5 cm
Explanation:
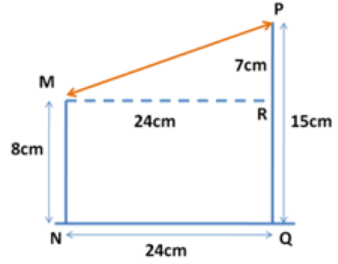
Let MN = Ramesh's fort & PQ = Suresh's fort
From the diagram we can see that
MR = 24 cm & PR = 15 - 8 = 7 cm
By Pythagoras theorem,
Hypotenuse2 = (side1)2 + (side2)2
$$\eqalign{ & {\text{MP}} = \sqrt {{{24}^2} + {7^2}} \cr & {\text{MP}} = 25\,{\text{cm}} \cr} $$
9. A and B are standing on ground 50 meters apart. The angles of elevation for these two to the top of a tree are 60° and 30°. What is height of the tree?
a) $$50\sqrt 3 \,{\text{m}}$$
b) $$\frac{{25}}{{\sqrt 3 }}\,{\text{m}}$$
c) $$25\sqrt 3 \,{\text{m}}$$
d) $$\frac{{25}}{{\sqrt 3 - 1}}\,{\text{m}}$$
Explanation:
$$\eqalign{ & {\text{In}}\,\Delta PBQ,\,\tan {60^ \circ } = \frac{{PQ}}{{BQ}} \cr & BQ = \frac{{PQ}}{{\sqrt 3 }} \cr & {\text{In}}\,\Delta PAQ,\,\tan {30^ \circ } = \frac{{PQ}}{{AQ}} \cr & \frac{1}{{\sqrt 3 }} = \frac{{PQ}}{{50 + BQ}} \cr & PQ = \frac{{50 + BQ}}{{\sqrt 3 }} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{50 + \frac{{PQ}}{{\sqrt 3 }}}}{{\sqrt 3 }} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{50\sqrt 3 + PQ}}{{\sqrt 3 \times \sqrt 3 }} \cr & 3PQ = 50\sqrt 3 + PQ \cr} $$
$$ PQ = 25\sqrt 3 \,{\text{m}} = $$ Height of tree
10.There is a tower of 10m between two parallel roads. The angles of depression of the roads from the top of the tower are 30° and 45°. How far are the roads from each other?
a) 27.32 m
b) 29.56 m
c) $$20\sqrt 3 \,{\text{m}}$$
d) $$\frac{{10}}{{\sqrt 3 }}\,{\text{m}}$$
Explanation:

Angle of Depression = Angle of Elevation
Tower PS = 10 m in height
$$\eqalign{ & {\text{tan}}{45^ \circ } = 1 = \frac{{PS}}{{RS}} \cr & PS = RS = 10 \cr & \tan {30^ \circ } = \frac{1}{{\sqrt 3 }} = \frac{{PS}}{{SQ}} = \frac{{10}}{{SQ}} \cr & SQ = 10\sqrt 3 \cr & RQ = RS + SQ \cr & \,\,\,\,\,\,\,\,\,\,\, = 10 + 10\sqrt 3 \cr & \,\,\,\,\,\,\,\,\,\,\, = 27.32\,{\text{m}} \cr} $$