1. If a 30 m ladder is placed against a 15 m wall such that it just reaches the top of the wall, then the elevation of the wall is equal to-
a) 45°
b) 30°
c) 60°
d) 50°
Explanation:
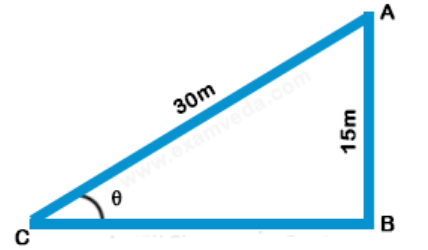
$$\eqalign{ & {\text{AC = 30 meter}} \cr & {\text{AB = 15 meter}} \cr & \angle {\text{ACB}} = \theta \cr & \sin \theta = \frac{{AB}}{{AC}} = \frac{{15}}{{30}} = \frac{1}{2} \cr & \sin \theta = \sin {30^ \circ } \cr & \theta = {30^ \circ } \cr} $$
2. The angles of elevation of the top of from two points P and Q at distance $${{m^2}}$$ and $${{n^2}}$$ respectively, from the base and in the same straight line with it are complementary. The height of the tower is-
a) $${\left( {mn} \right)^{\frac{1}{2}}}$$
b) $$m{n^{\frac{1}{2}}}$$
c) $${m^{\frac{1}{2}}}n$$
d) $$mn$$
Explanation:
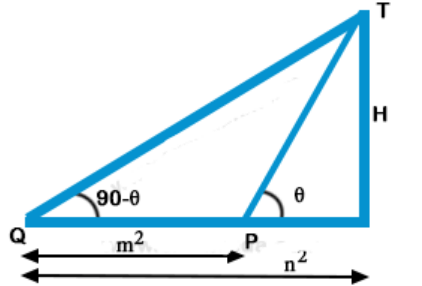
$$\eqalign{ & {\text{tan }}\theta = \frac{H}{{{m^2}}} \cr & \tan \left( {90^ \circ - \theta } \right) = \frac{H}{{{n^2}}} \cr & \cot \theta = \frac{H}{{{n^2}}} \cr & \tan \theta .\cot \theta = \frac{H}{{{m^2}}} \times \frac{H}{{{n^2}}} \cr & \frac{H}{{{m^2}}} \times \frac{H}{{{n^2}}} = 1 \cr & {H^2} = {m^2}{n^2} \cr & H = mn \cr} $$
3. A boy is standing at the top of the tower and another boy is at the ground at some distance from the foot of the tower, then the angle of elevation and depression between the boys when both look at a each other will be-
a) Equal
b) Angle of elevation will be greater
c) Cannot be predicted for relation
d) Angle of depression will be greater
Explanation:
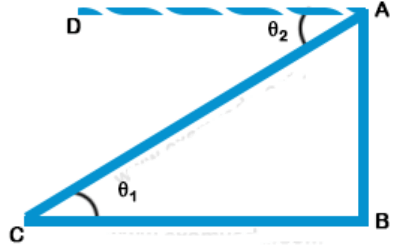
$$\eqalign{ & {\text{Here, AD is parallel to BC and AC is a transversal}}{\text{.}} \cr & {\theta _1} = {\theta _2} \cr} $$
4.The angle of elevation of a cloud from a point 200 m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. The height of the cloud is-
a) 200 m
b) 300 m
c) 400 m
d) 600 m
Explanation:
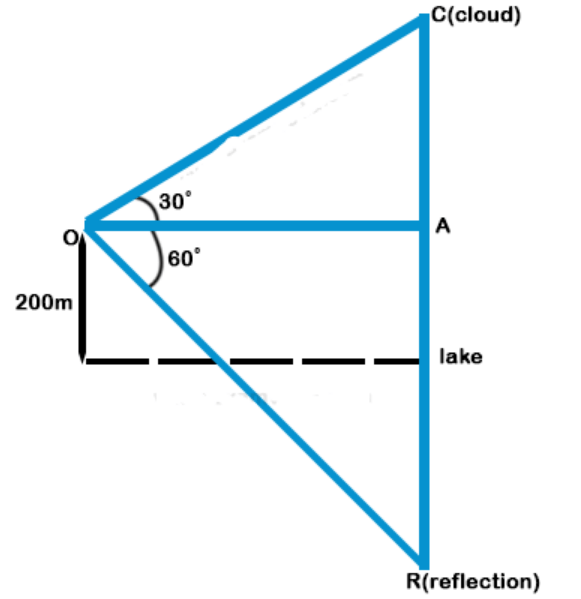
$$\eqalign{ & {\text{Let, }}AC = H{\text{ }}m \cr & OA = {\text{ }}a{\text{ }}m \cr & \tan {\text{ }}{30^ \circ } = \frac{1}{{\sqrt 3 }} = \frac{H}{a} \cr} $$
$$\tan {60^ \circ } = \sqrt 3 $$ $$ = \frac{{H + 200 + 200}}{a}$$
$$\eqalign{ & \frac{{H + 400}}{{\sqrt 3 H}} = \sqrt 3 \cr & H + 400 = 3H \cr & 2H = 400\,m \cr & H = 200\,m \cr} $$
Height of cloud above lake = 200 m
5. A man is watching from the top of tower a boat speeding away from the tower. The boat makes an angle of depression of 45° with the man’s eye when at a distance of 60 meters from the tower. After 5 seconds, the angle of depression becomes 30°. What is the approximate speed of the boat, assuming that it is running in still water?
a) 32 kmph
b) 36 kmph
c) 38 kmph
d) 40 kmph
Explanation:
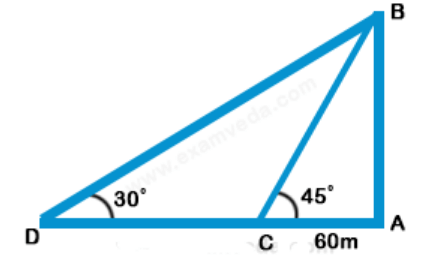
Let AB be the tower and C and D be the two positions of the boats.
Then, $$\angle {\text{ACB = }}{45^ \circ },$$ $$\angle ADB = {30^ \circ }$$ and AC = 60 m
Let, AB = h
$$\eqalign{ & {\text{Then,}}\frac{{AB}}{{AC}} = \tan {45^ \circ } = 1 \cr & \Rightarrow AB = AC \cr & \Rightarrow h = 60\,m \cr & {\text{And}}\frac{{AB}}{{AD}} = \tan {30^ \circ } = \frac{1}{{\sqrt 3 }} \cr & AD = \left( {AB \times \sqrt 3 } \right) \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = 60\sqrt 3 \,m \cr & CD = \left( {AD - AC} \right) \cr & \,\,\,\,\,\,\,\,\,\,\, = 60\left( {\sqrt 3 - 1} \right)\,m \cr & {\text{Hence, required speed }} \cr & {\text{ = }}\left[ {\frac{{60\left( {\sqrt 3 - 1} \right)}}{5}} \right]{\text{m/s}} \cr & {\text{ = }}\left( {12 \times 0.73} \right){\text{m/s}} \cr & = \left( {12 \times 0.73 \times \frac{{18}}{5}} \right){\text{km/hr}} \cr & = {\text{31}}{\text{.5km/hr }} \approx {\text{ 32km/hr}} \cr} $$
6. The length of shadow of a tower on the plane ground is $$\sqrt 3 $$ times the height of the tower. The angle of elevation of sun is
a) 45°
b) 30°
c) 60°
d) 90°
Explanation: Let AB be tower and BC be its shadow
Let AB = x
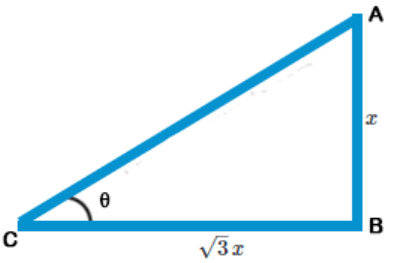
$$\eqalign{ & {\text{Then}}\,BC = \sqrt 3 \times x = \sqrt 3 \,x \cr & \tan \theta = \frac{{AB}}{{BC}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{x}{{\sqrt 3 \,x}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{{\sqrt 3 }} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \tan {30^ \circ } \cr & \theta = {30^ \circ } \cr} $$
Angle of elevation of the sun$${\text{ = }}{30^ \circ }$$
7. The length of the shadow of a tower standing on level ground is found to 2x meter longer when the sun’s elevation is 30° than when it was 45 °. The height of the tower in meters is
a) $$\left( {\sqrt 3 + 1} \right)\,x$$
b) $$\left( {\sqrt 3 - 1} \right)\,x$$
c) $$2\sqrt 3 \,x$$
d) $$3\sqrt 2 \,x$$
Explanation: AB is a tower
BD and BC are its shadows and CD = 2x
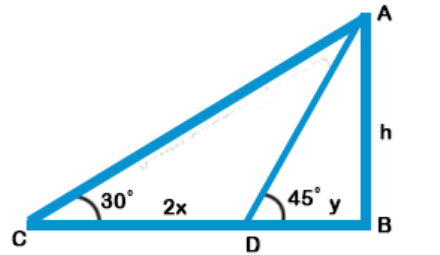
$$\eqalign{ & \tan {45^ \circ } = \frac{{AB}}{{DB}} \cr & \Rightarrow 1 = \frac{h}{y} \Rightarrow y = h \cr & {\text{and}}\tan {30^ \circ } = \frac{{AB}}{{CB}} \cr & \frac{1}{{\sqrt 3 }} = \frac{h}{{2x + y}} \cr & 2x + y = \sqrt 3 \,h \cr & \sqrt 3 \,h - h = 2x \cr & h\left( {\sqrt 3 - 1} \right) = 2x \cr & \Rightarrow h = \frac{{2x}}{{\sqrt 3 - 1}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{2x\left( {\sqrt 3 + 1} \right)}}{{\left( {\sqrt 3 - 1} \right)\left( {\sqrt 3 + 1} \right)}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{2x\left( {\sqrt 3 + 1} \right)}}{{3 - 1}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{2x\left( {\sqrt 3 + 1} \right)}}{2} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = x\left( {\sqrt 3 + 1} \right) \cr} $$
8. If the angle of elevation of the top of a tower from two points distant a and b from the base and in the same straight line with It are complementary, then the height of the tower is
a) $$ab$$
b) $$\sqrt {ab} $$
c) $$\frac{a}{b}$$
d) $$\sqrt {\frac{a}{b}} $$
Explanation: Let AB be the tower and P and Q are two points such that PB = a and QB = b and angles of elevation are $$\theta $$ and (90° – $$\theta $$)
Let height of tower = h
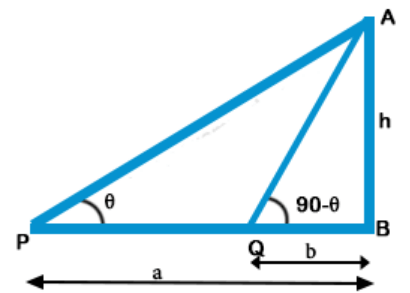
$$\eqalign{ & {\text{Then}}\,{\text{in}}\,{\text{right}}\,\Delta APB, \cr & \tan \theta = \frac{{{\text{Perpendicular}}}}{{{\text{Base}}}} = \frac{{AB}}{{PB}} \cr & = \frac{h}{a}\,............\left( {\text{i}} \right) \cr & {\text{Similarly in right }}\Delta AQB, \cr & \tan \left( {{{90}^ \circ } - \theta } \right) = \frac{{AB}}{{QB}} = \frac{h}{b} \cr & \Rightarrow \cot \theta = \frac{h}{b}\,...........\left( {{\text{ii}}} \right) \cr & {\text{Multiplying }}\left( {\text{i}} \right){\text{ and }}\left( {{\text{ii}}} \right) \cr & \tan \theta \cot \theta = \frac{h}{a} \times \frac{h}{b} \cr & 1 = \frac{{{h^2}}}{{ab}} \cr & {h^2} = ab \cr & h = \sqrt {ab} \cr & {\text{Height}}\,{\text{of}}\,{\text{tower}} = \sqrt {ab} \cr} $$
9. The angle of elevation of the top of a lighthouse 60 m high, from two points on the ground on its opposite sides are 45° and 60°. What is the distance between these two points?
a) 45 m
b) 30 m
c) 103.8 m
d) 94.6 m
Explanation:
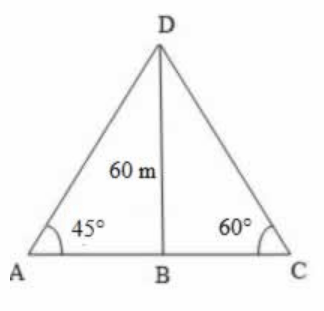
Let BD be the lighthouse and A and C be the two points on ground.
Then, BD, the height of the lighthouse = 60 m
∠BAD = 45°, ∠BCD = 60°
$$\eqalign{ & \tan {45^ \circ } = \frac{{BD}}{{BA}} \cr & 1 = \frac{{60}}{{BA}} \cr & BA = 60\,m\,........\left( {\text{i}} \right) \cr & \tan {60^ \circ } = \frac{{BD}}{{BC}} \cr & \sqrt 3 = \frac{{60}}{{BC}} \cr & \Rightarrow BC = \frac{{60}}{{\sqrt 3 }} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{60 \times \sqrt 3 }}{{\sqrt 3 \times \sqrt 3 }} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{60\sqrt 3 }}{3} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 20\sqrt 3 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 20 \times 1.73 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 34.6\,m\,..........\left( {{\text{ii}}} \right) \cr} $$
Distance between the two points A and C
= AC = BA + BC
= 60 + 34.6 [ Substituted value of BA and BC from (i) and (ii)]
= 94.6 m
10. On the same side of a tower, two objects are located. Observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 600 m, the distance between the objects is approximately equal to :
a) 272 m
b) 284 m
c) 288 m
d) 254 m
Explanation:
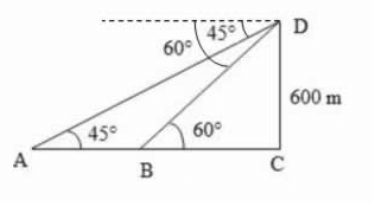
Let DC be the tower and A and B be the objects as shown above.
Given that DC = 600 m, ∠DAC = 45°, ∠DBC = 60°
$$\eqalign{ & \tan {60^ \circ } = \frac{{DC}}{{BC}} \cr & \sqrt 3 = \frac{{600}}{{BC}} \cr & BC = \frac{{600}}{{\sqrt 3 }}\,..........\,\left( {\text{i}} \right) \cr & \tan {45^ \circ } = \frac{{DC}}{{AC}} \cr & 1 = \frac{{600}}{{AC}} \cr & AC = 600\,............\,\left( {{\text{ii}}} \right) \cr} $$
Distance between the objects
$$ = AC = \left( {AC - BC} \right)$$
$$ = 600 - \frac{{600}}{{\sqrt 3 }}$$ [ from (1) and (ii)]
$$\eqalign{ & = 600\left( {1 - \frac{1}{{\sqrt 3 }}} \right) \cr & = 600\left( {\frac{{\sqrt 3 - 1}}{{\sqrt 3 }}} \right) \cr & = 600\left( {\frac{{\sqrt 3 - 1}}{{\sqrt 3 }}} \right) \times \frac{{\sqrt 3 }}{{\sqrt 3 }} \cr & = \frac{{600\sqrt 3 \left( {\sqrt 3 - 1} \right)}}{3} \cr & = 200\sqrt 3 \left( {\sqrt 3 - 1} \right) \cr & = 200\left( {3 - \sqrt 3 } \right) \cr & = 200\left( {3 - 1.73} \right) \cr & = 254\,m \cr} $$