1. Find the current I (mA) in the circuit shown below.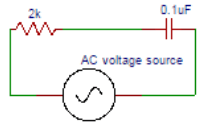
a) 2.66
b) 3.66
c) 4.66
d) 5.66
Explanation:The term current is the ratio of voltage to the impedance. The current I (mA) in the circuit is current I = VS / Z = 10/3760.6 = 2.66mA
2. Find the voltage across the capacitor in the circuit shown below.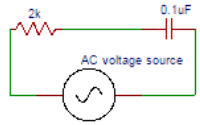
a) 7
b) 7.5
c) 8
d) 8.5
Explanation: The voltage across the capacitor in the circuit is capacitor voltage = 2.66×10-3×3184.7 =8.47V.
3. Determine the voltage across the resistor in the circuit shown below.
a) 3
b) 4
c) 5
d) 6
Explanation: The voltage across the resistor in the circuit resistive voltage = 2.66×10-3×3184.7 = 5.32V.
4.In the circuit shown below determine the total impedance.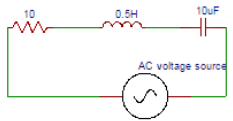
a) 161
b) 162
c) 163
d) 164
Explanation: Reactance across capacitor = 1/(6.28×50×10×10-6) = 318.5Ω.
Reactance across inductor = 6.28×0.5×50=157Ω. In rectangular form, Z = (10+j157-j318.5) Ω = (10-j161.5)Ω. Magnitude=161.8Ω.
5. Find the current in the circuit shown below.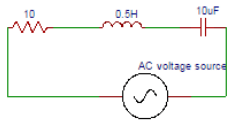
a) 0.1
b) 0.2
c) 0.3
d) 0.4
Explanation: The term current is the ratio of voltage to the impedance. The current in the circuit is current I=VS/Z = 50/161.8 = 0.3A.
6. A signal generator supplies a sine wave of 20V, 5 kHz to the circuit as shown. Determine total current IT.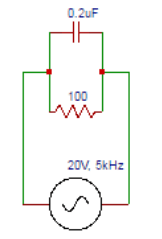
a) 0.21∠33⁰
b) 0.22∠33⁰
c) 0.23∠33⁰
d) 0.24∠33⁰
Explanation: Capacitive reactance = 1/(6.28×5×103×0.2×10-6)=159.2Ω.Current in the resistance branch IR=VS/R=20/100 = 0.2A.Current in capacitive branch IC=VS/XC = 20/159.2 = 0.126A.Total current IT = (IR+j IC) A = (0.2+j0.13) A. In polar form, IT = 0.24∠33⁰ A.
7. Find the phase angle in the circuit shown below.
a) 31⁰
b) 32⁰
c) 33⁰
d) 34⁰
Explanation: We obtained IT = 0.24∠33⁰ A, the phase angle between applied voltage and current is 33⁰. The phase angle between the applied voltage and total current is 33⁰
8. Determine the total impedance in the circuit.
a) 73.3∠33⁰
b) 83.3∠-33⁰
c) 83.3∠33⁰
d) 73.3∠-33⁰
Explanation: Z = VS/IT = 20∠0⁰ / 0.24∠33⁰ = 83.3∠-33⁰Ω. The phase angle indicates that the total line current is 0.24 A and leads the voltage by 33⁰.
9. A 50Ω resistor is connected in parallel with an inductive reactance of 30Ω. A 20V signal is applied to the circuit. Find the line current in the circuit.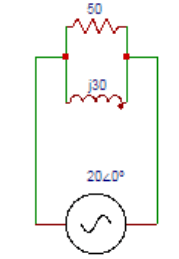
a) 0.77∠-58.8⁰
b) 0.77∠58.8⁰
c) 0.88∠-58.8⁰
d) 0.88∠58.8⁰
Explanation: Since the voltage across each element is the same as the applied voltage, the current in resistive branch is IR = VS/R = 20∠0⁰/50∠0⁰=0.4A. Current in the inductive branch is IL = VS/XL = 20∠0⁰/30∠90⁰= 0.66∠-90⁰. Total current is IT = 0.4-j0.66 = 0.77∠-58.8⁰
10. Determine total impedance in the circuit shown below.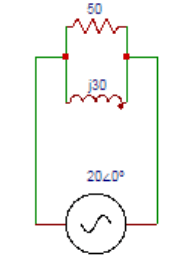
a) 25∠-58.8⁰
b) 25∠-58.8⁰.
c) 26∠-58.8⁰.
d) 26∠58.8⁰.
Explanation: The current lags behind the voltage by 58.8⁰. Total impedance Z = VS/IT = 20∠0⁰ / 0.77∠-58.8⁰ = 25.97∠-58.8⁰Ω. So the total impedance in the circuit shown is 25.97∠-58.8⁰Ω.