1. Determine Z in the figure shown below.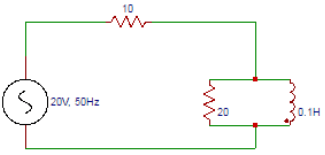
a) 26∠-20.5⁰
b) 26∠20.5⁰
c) 25∠-20.5⁰
d) 25∠20.5⁰
Explanation: First the inductive reactance is calculated. XL=6.28 x 50 x 0.1 = 31.42Ω. In figure the 10Ω resistance is in series with the parallel combination of 20Ω and j31.42Ω. ZT = 10 + (20)(j31.42)/(20+j31.42)=24.23+j9.06=25.87∠20.5⁰
2. Find IT in the figure shown below.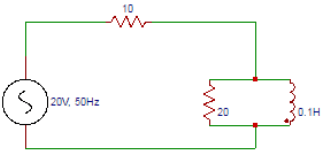
a) 0.66∠-20.5⁰
b) 0.66∠20.5⁰
c) 0.77∠20.5⁰
d) 0.77∠-20.5⁰
Explanation: The current lags behind the applied voltage by 20.5⁰. Total current IT = VS/ZT = 20/25.87∠20.5o=0.77∠-20.5o
3. Find the phase angle θ in the circuit shown below.
a) 20.5⁰
b) 20⁰
c) 19.5⁰
d) 19⁰
Explanation: As IT = 0.77∠-20.5o, the phase angle θ between the voltage and the current in the circuit is 20.5⁰
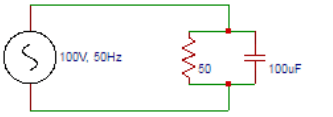
4. Find the impedance in the circuit shown below.
a) 25
b) 26
c) 27
d) 28
Explanation:Capacitive reactance XC = 1/2πfC = 1/(6.28×50×100×10-6)=31.83Ω. Capacitive susceptance BC = 1/XC = 1/31.83 = 0.031S. Conductance G=1/R = 1/50 = 0.02S. Total admittance Y=√(G2+Bc2)=√(0.022+0.0312)=0.037S. Total impedance Z = 1/Y = 1/0.037 = 27.02Ω.
5. Determine the phase angle in the circuit shown below.
a) 56⁰
b) 56.5⁰
c) 57.5⁰
d) 57⁰
Explanation: Phase angle θ=tan-1(R/Xc). Resistance R = 50Ω and capacitive reactance Xc = 31.83Ω. So the phase angle in the circuit = tan-1(50/31.83)=57.52⁰.
6. In purely resistive circuit, energy delivered by source is ____________ by resistance.
a) dissipated in the form of heat
b) stored as electric field
c) stored as magnetic field
d) returned to source
Explanation: In purely resistive circuit, energy delivered by source is dissipated in the form of heat by resistance and is not stored as either electric field or magnetic field.
7. In inductor, the energy delivered by source is ____________ by inductor.
a) stored as magnetic field
b) dissipated in the form of heat
c) returned to source
d) stored as electric field
Explanation: In inductor, the energy delivered by source is stored as magnetic field by inductor and is not dissipated in the form of heat or stored as electric field.
8. In capacitor, the energy delivered by source is ____________ by capacitor.
a) returned to source
b) dissipated in the form of heat
c) stored as electric field
d) stored as magnetic field
Explanation:In capacitor, the energy delivered by source is stored as electric field by capacitor and is not stored as magnetic field or dissipated in the form of heat.
9. If there is complex impedance in a circuit, part of energy is ____________ by reactive part and part of its energy is ____________ by the resistance.
a) alternately stored and returned, alternately stored and returned
b) alternately stored and returned, dissipated
c) dissipated, alternately stored and returned
d) dissipated, dissipated
Explanation: If there is complex impedance in a circuit, part of energy is alternately stored and returned by reactive part and part of its energy is dissipated by the resistance. The amount of energy dissipated is determined by relative values of resistance and reactance.
10. The equation of instantaneous power is?
a) P (t) = (VmIm/2)(cos(2ωt+θ)+sinθ)
b) P (t) = (VmIm/2)(sin(2ωt+θ)+cosθ)
c) P (t) = (VmIm/2)(cos(2ωt+θ)+cosθ)
d) P (t) = (VmIm/2)(sin(2ωt+θ)+sinθ)
Explanation: The equation of instantaneous power is P (t) = (VmIm/2)(cos(2ωt+θ)+cosθ). It consists of two parts. One is a fixed part and the other is time varying which has frequency twice that of the voltage or current wave forms.