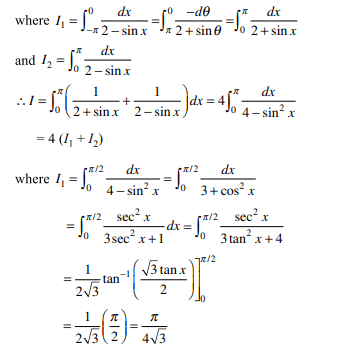PrepBharat

1.If \[I=\int\frac{dx}{\cos^{4}x-\cos^{2}x\sin^{2}x+\sin^{4}x}\]
then I is equals
a) \[2\tan^{-1}\left(\frac{\tan2x}{2}\right)+C\]
b) \[\tan^{-1}\left(\frac{\tan2x}{\sqrt{2}}\right)+C\]
c) \[\tan^{-1}\left(\frac{\tan2x}{2}\right)+C\]
d) \[\sqrt{2}\tan^{-1}\left(\frac{\tan2x}{\sqrt{2}}\right)+C\]

View Answer

2. If \[I=\int\frac{dx}{\sqrt{\left(2 x-x^{2}\right)^{3}}}\]
then I is equals
a) \[\frac{2x-1}{\sqrt{x\left(2-x\right)}}+C\]
b) \[\frac{x-1}{\sqrt{x\left(2-x\right)}}+C\]
c) \[\frac{x+1}{\sqrt{x\left(2-x\right)}}+C\]
d) \[\frac{1-x}{\sqrt{x\left(2-x\right)}}+C\]

View Answer

3.If \[I=\int\frac{dx}{\left(1+\sqrt{x}\right)\sqrt{x-x^{2}}}\]
then I is equals
a) \[\frac{2\left(\sqrt{x}+1\right)}{\sqrt{1-x}}+C\]
b) \[\frac{2\left(\sqrt{x}-1\right)}{\sqrt{1-x}}+C\]
c) \[\frac{2\left(1-\sqrt{x}\right)}{\sqrt{x\left(1-x\right)}}+C\]
d) \[\frac{2\left(\sqrt{x}-1\right)}{\sqrt{x\left(1-x\right)}}+C\]

View Answer

4. If \[I=\int\left(\sqrt{\frac{a+x}{a-x}}+\sqrt{\frac{a-x}{a+x}}\right)dx\]
then I is equals
a) \[2\sin^{-1}\left(\frac{x}{a}\right)+C\]
b) \[2a\sin^{-1}\left(\frac{x}{a}\right)+C\]
c) \[2\cos^{-1}\left(\frac{x}{a}\right)+C\]
d) \[2a\cos^{-1}\left(\frac{x}{a}\right)+C\]

View Answer

5. If \[I=\int\frac{dx}{x^{4}\sqrt{1+x^{2}}}\]
then I is equals
a) \[\frac{\sqrt{x^{2}+1}}{x}-\frac{1}{2x^{2}}+C\]
b) \[\frac{\sqrt{1+x^{2}}}{x}-\frac{1}{2x^{3}}+C\]
c) \[-\frac{\sqrt{1+x^{2}}}{x}+\frac{2x}{\sqrt{1+x^{2}}}+C\]
d) \[\frac{\sqrt{1+x^{2}}}{x}-\frac{2x}{\sqrt{1+x^{2}}}+C\]

View Answer

6. If \[I=\int\frac{\sin\left( x+\alpha\right)+\cos x}{\sin\left(x-\alpha\right)}dx\]
then I is equals
a) \[2\cos\alpha\left(1+\sin\alpha\right)\log\mid\sin\left(x-\alpha\right)\mid+\left(\cos2\alpha+\cos\alpha\right)x+C\]
b) \[\cos\alpha\left(1+2\sin\alpha\right)\log\mid\sin\left(x-\alpha\right)\mid+\left(\cos2\alpha-\sin\alpha\right)x+C\]
c) \[2\sin\alpha\left(1+\cos\alpha\right)\log\mid\sin\left(x-\alpha\right)\mid+\left(\cos2\alpha+\cos\alpha\right)x+C\]
d) \[2\tan\alpha\left(1+\cos\alpha\right)\log\mid\sin\left(x-\alpha\right)\mid+\left(\cos\alpha-\sin\alpha\right)x+C\]

View Answer

7. If \[I=\int e^{x}\frac{x^{3}+3x^{2}+4}{\left( x+1\right)^{3}}dx\]
then I is equals
a) \[ e^{x}\left(\frac{x^{2}-x+1}{\left( x+1\right)^{2}}\right)+C\]
b) \[ e^{x}\left(\frac{x^{2}-x+2}{\left( x+1\right)^{2}}\right)+C\]
c) \[ e^{x}\left(\frac{x^{2}+2x-2}{\left( x+1\right)^{2}}\right)+C\]
d) \[ e^{x}\left(\frac{x^{2}+2x-1}{\left( x+1\right)^{2}}\right)+C\]

View Answer

8. If \[I=\int\tan x\tan2x\tan3x dx\]
then I is equals
a) \[\log \mid \cos x\mid +\left(1/2\right)\log \mid \cos 2x\mid+\left(1/3\right)\log\mid\cos 3x\mid+C\]
b) \[\log \mid \cos x\mid -\left(1/2\right)\log \mid \cos 2x\mid-\left(1/3\right)\log\mid\cos 3x\mid+C\]
c) \[\log \mid \cos x\mid +\left(1/2\right)\log \mid \cos 2x\mid-\left(1/3\right)\log\mid\cos 3x\mid+C\]
d) none of these

View Answer

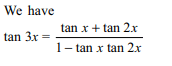
9. If \[I=\int\frac{dx}{\left(2\sin x+\sec x\right)^{4}}\]
then I is equals
a) \[-\frac{1}{5\tan^{5}x}+\frac{1}{3\tan^{6}x}-\frac{2}{7\tan^{7}x}+C\]
b) \[\frac{1}{5\tan^{5}x}+\frac{1}{3\tan^{6}x}-\frac{1}{\left(2\sin x+\sec x \right)^{3}}+C\]
c) \[\frac{-1}{3\left(2\sin x+\sec x\right)^{3}}+\tan^{-1}\left(3\sqrt{\tan x}\right)+C\]
d) \[\frac{-1}{3\left(2\sin x+\sec x \right)^{3}}-\tan^{-1}\left(3\sqrt{\tan x}\right)+C\]

View Answer

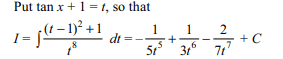
10. If \[I=\int e^{x}\left(\frac{x+2}{x+4}\right)^{2}dx\]
then I is equals
a) \[ \frac{x}{x+4}e^{x}+C\]
b) \[ \frac{x-2}{x+4}e^{x}+C\]
c) \[ \frac{x+1}{x+4}e^{x}+C\]
d) \[ \frac{x-1}{x+4}e^{x}+C\]

View Answer

11.Let \[\int\frac{x^{1/2}}{\sqrt{1-x^{3}}}dx=\frac{2}{3}gof\left(x\right)+C\]
(C being the constant of integration) then
a) \[f\left(x\right)=\sqrt{3}\]
b) \[f\left(x\right)=x^{3/2}\]
c) \[g\left(x\right)=\sin^{-1}x\]
d) Both b and c

View Answer

12. If \[I=\int\left(\tan x\right)^{1/3}dx =A\log\frac{t^{4}-t^{2}+1}{\left(t^{2}+1\right)^{2}}+B\tan^{-1}\frac{2t^{2}-1}{2\sqrt{3}}+C\]
where \[t=\tan^{1/3}x\]    then
a) A = 1/4
b) \[B=\sqrt{3}/2\]
c) A = -1/4
d) Both a and b

View Answer

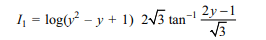
13. If \[I=\int\frac{\sin x+\sin^{3} x}{\cos 2x}dx=A\cos x+B\log \mid f\left(x\right)\mid+C\]
then
a) \[A = 1/4, B = – 1/2, f\left(x\right) =\frac{\sqrt{2}\cos x-1}{\sqrt{2}\cos x+1}\]
b) \[A = 1/2, B = -3/4 \sqrt{2}\]
c) \[A = -1/2, B = 3/\sqrt{5}, f\left(x\right) =\frac{\sqrt{2}\cos x+1}{\sqrt{2}\cos x-1}\]
d) Both b and c

View Answer

14. The value of the integral \[\int\frac{\log\left(x+1\right)-\log x}{x\left(x+1\right)}dx\]
is
a) \[-\left(1/2\right)\left(\log x+1\right)^{2}-\left(1/2\right)\left(\log x\right)^{2}+\log\left(x+1\right) \log x+C\]
b) \[-\left[\left(\log x+1\right)^{2}-\left(\log x\right)^{2}\right]+\log\left(x+1\right) \log x+C\]
c) \[C -\left(1/2\right) (\log\left(1+1/x\right)^{2}\]
d) Both a and c

View Answer

15. If \[\int\frac{xe^{x}}{\sqrt{1+e^{x}}}dx=f\left(x\right)\sqrt{1+e^{x}}-2\log g\left(x\right)+C\]
then
a) f (x) = x – 1
b) f (x) = 2(x – 2)
c) \[g\left(x\right)=\frac{\sqrt{1+e^{x}}-1}{\sqrt{1+e^{x}}+1}\]
d) Both b and c

View Answer

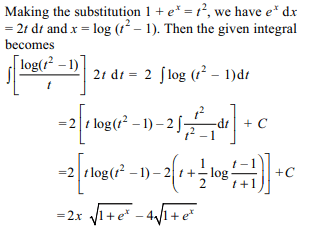
16. If \[\int xe^{-5x^{2}}\sin4x^{2} dx=ke^{-5x^{2}}\left(A \sin 4x^{2}+B\cos4x^{2}\right)+C\]
then
a) K = – 1/82
b) K = 1/82
c) A = 5
d) Both a and c

View Answer

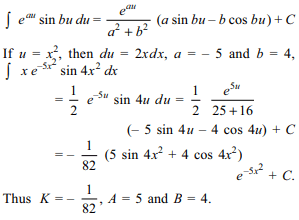
17. If \[\int f\left(x\right)dx=\frac{3}{55}\sqrt[3]{\tan^{5}x}\left(5\tan^{2} x+11\right)+C\]
then f(x) is equal to
a) \[\sqrt[3]{\sin^{2} x\cos^{-14} x}\]
b) \[\sqrt[3]{\tan^{2} x\left(1+\tan^{2} x\right)^{6}}\]
c) \[\sqrt[3]{\cos^{2} x\sin^{-14} x}\]
d) Both a and b

View Answer

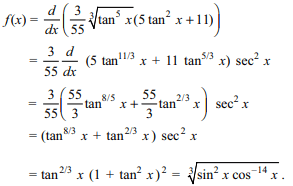
18. The value of \[\int_{1}^{\sqrt{3}} \frac{1}{x^{2}}\log\sqrt{1+x^{2}}dx\]
is
a) \[\frac{\sqrt{3}-2}{2\sqrt{3}}\log 2+\frac{\pi}{8}\]
b) \[\frac{\sqrt{3}-2}{2\sqrt{3}}\log 2+\frac{\pi}{12}\]
c) \[\frac{1}{4}\log 2\]
d) \[\frac{\sqrt{3}-2}{\sqrt{3}}\log 2+\frac{\pi}{12}\]

View Answer

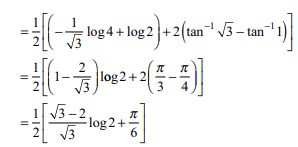
19. For a, b > 0, the value of\[\int_{0}^{1} \frac{\log\frac{\left(x+a\right)^\left(x+a\right)}{\left(x+b\right)^\left(x+b\right)}}{\left(x+a\right)\left(x+b\right)\log\left(x+a\right)\log\left(x+b\right)}dx\]
is equal to
a) \[\log\left(\frac{1+a}{1+b}\right)\frac{\log a}{\log b}\]
b) \[\frac{\log\left(1+a\right)\log a}{\log\left(1+b\right)\log b}\]
c) \[\log\left(\frac{\log\left(1+a\right)\log b}{\log\left(1+b\right)\log a}\right)\]
d) \[\log\frac{\log\left(1+b\right)\log a}{\log\left(1+a\right)\log b}\]

View Answer

20. If \[\alpha=\int_{0}^{\pi/3} \frac{dx}{1+\sin x}\]
and \[P\left(x\right)=x^{3}+2x^{2}+4\]
then the value of \[P\left(\alpha\right)\]   is
a) \[\sqrt{3}+1\]
b) \[2\left(\sqrt{3}+1\right)\]
c) \[2\left(\sqrt{3}-1\right)\]
d) \[4\left(\sqrt{3}-1\right)\]

View Answer

21.Let f, g be continuously differentiable functions from R⁺ to R⁺ then the value of
\[\int_{a}^{b} \frac{f\left(x\right)g'\left(x\right)-f'\left(x\right)}{f\left(x\right)+e^{g\left(x\right)}}dx\]
is equal to
a) \[\log\left(\frac{e^{-g\left(b\right)}f\left(b\right)+1}{e^{-g\left(a\right)}f\left(a\right)+1}\right)\]
b) \[\log\left(\frac{e^{-g\left(a\right)}f\left(a\right)+1}{e^{-g\left(b\right)}f\left(b\right)+1}\right)\]
c) \[\log\left(\frac{e^{-g\left(a\right)}f\left(b\right)+1}{e^{-g\left(a\right)}f\left(a\right)+1}\right)\]
d) \[\log\left(\frac{e^{-g\left(b\right)}f\left(a\right)+1}{e^{-g\left(a\right)}f\left(b\right)+1}\right)\]

View Answer

22. The value of \[I= \int_{0}^{\pi} \frac{x\sin x}{\cos 4x+4\cos 2x+11}dx\]
is
a) \[\frac{\pi}{32}\left(\pi-\log\left(1+2\sqrt{2}\right)\right)\]
b) \[\frac{\pi}{32\sqrt{2}}\left(\pi-\log\left(3-2\sqrt{2}\right)\right)\]
c) \[\frac{\pi}{16}\left(\pi-\log\left(3+2\sqrt{2}\right)\right)\]
d) \[\frac{\pi}{16}\left(\pi-\log\left(3-2\sqrt{2}\right)\right)\]

View Answer

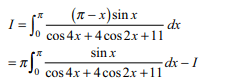
23.If \[I=\int_{-\pi/6}^{\pi/6} \frac{\pi+4x^{5}}{1-\sin\left(\mid x \mid+\pi/6\right)}dx\]
then I equals
a) \[4\pi\]
b) \[2\pi+1/\sqrt{3}\]
c) \[2\pi-\sqrt{3}\]
d) \[4\pi+\sqrt{3}-1\]

View Answer

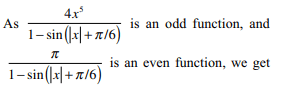
24. If \[I=\int_{-3}^{2} \left(\mid x+1\mid+\mid x+2\mid+\mid x-1\mid\right)dx\]
then I equals
a) \[\frac{31}{2}\]
b) \[\frac{35}{2}\]
c) \[\frac{37}{2}\]
d) \[\frac{39}{2}\]

View Answer

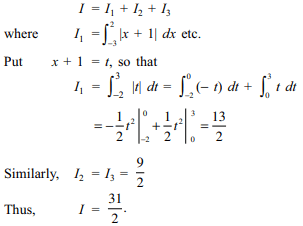
25. If \[I=\int_{0}^{1.7} \left[x^{2}\right]dx\]
then I equals
a) \[2.4+\sqrt{2}\]
b) \[2.4-\sqrt{2}\]
c) \[3.4+\sqrt{2}\]
d) \[2.4-1/\sqrt{2}\]

View Answer

26.The value of \[I=\int_{-2}^{0} \left[x^{3}+3x^{2}+3x+\left(x+1\right)\cos\left(x+1\right)\right]dx\]
is
a) -4
b) -3
c) -2
d) -1

View Answer

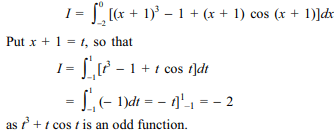
27. If \[I=\int_{0}^{\pi} e^{\mid\left(1/2\right)\cos x \mid}\left\{2\sin\left(\frac{1}{2}\cos x\right)+3\cos\left(\frac{1}{2}\cos x\right)\right\}\sin x dx\]
then I equals
a) \[7\sqrt{e}\cos \left(1/2\right)\]
b) \[7\sqrt{e}\left[\cos \left(1/2\right)-\sin\left(1/2\right)\right]\]
c) 0
d) \[6\left(\sqrt{e}\left(\cos\frac{1}{2}+\sin\frac{1}{2}\right)-1\right)\]

View Answer

28. If \[I=\int_{-2}^{2} \mid 1-x^{4}\mid dx\]
then I equals
a) 6
b) 8
c) 12
d) 21

View Answer

29. The value of \[\int_{-1}^{2} \mid \left[x\right]-\left\{x\right\}\mid dx\]
, where [x] is the greatest integer less then or equal to x and {x} is the fractional part of x is
a) 7/2
b) 5/2
c) 1/2
d) 3/2

View Answer

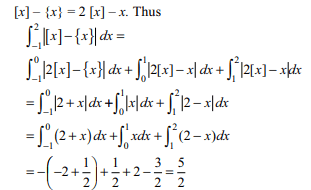
30. If \[I=\int_{2}^{3}\frac{2x^{5}+x^{4}-2x^{3}+2x^{2}+1}{\left(x^{2}+1\right)\left(x^{4}-1\right)}dx\]
then I equals
a) \[\frac{1}{2}\log 6+\frac{1}{10}\]
b) \[\frac{1}{2}\log 6-\frac{1}{10}\]
c) \[\frac{1}{2}\log 3-\frac{1}{10}\]
d) \[\frac{1}{2}\log 2+\frac{1}{10}\]

View Answer

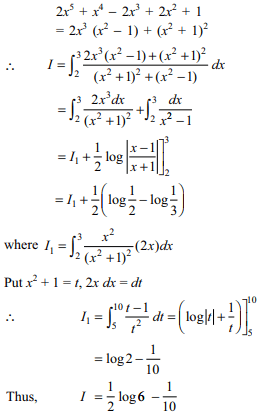
31. If \[I=\int_{0}^{\pi/2}\cos^{n}x\sin^{n}x dx=\lambda\int_{0}^{\pi/2} sin^{n}x dx\]
then \[\lambda\] equals
a) \[2^{-n+1}\]
b) \[2^{-n-1}\]
c) \[2^{-n}\]
d) \[2^{-1}\]

View Answer

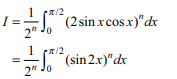
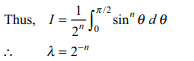
32. If \[I=\int_{0}^{\pi} \sin ^{3}x\left(1+2\cos x\right)\left(1+\cos x\right)^{2} dx\]
then I equals
a) \[\frac{4}{3}\]
b) \[\frac{2}{3}\]
c) \[\frac{8}{3}\]
d) 2

View Answer

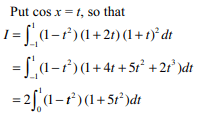
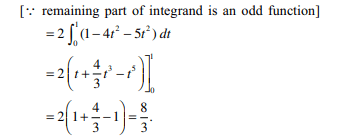
33.If \[I=\int_{1/3}^{3} \frac{1}{x}\sin \left(\frac{1}{x}-x\right)dx\]
then I equals
a) \[\sqrt{3}/2\]
b) \[\pi+\sqrt{3}/2\]
c) 0
d) \[\pi-\sqrt{3}/2\]

View Answer

34. If \[I=\int_{0}^{\pi/2} \frac{\sin 8 x\log \left(\cot x\right)}{\cos 2x})dx\]
then I equals
a) \[-\pi/2\]
b) \[\pi/3\]
c) - 1/3
d) 0

View Answer

35. If \[I=\int_{1/e}^{e} \mid\log x \mid \frac{dx}{x^{2}}\]
then I equals
a) 2
b) 2/e
c) 2(1-1/e)
d) 0

View Answer

36. If for \[ K\epsilon N,\]
\[\frac{\sin2kx}{\sin x}=2\left[\cos x+\cos3x+....+\cos\left(2k-1\right)x\right]\]
then value of \[I=\int_{0}^{\pi/2} \sin2kx\cot x dx\]
is
a) \[-\pi/2\]
b) 0
c) \[\pi/2\]
d) \[\pi\]

View Answer

37.The natural number \[n\left(\leq 5\right)\]   for which \[I_{n}=\int_{0}^{1} e^{x}\left(x-1\right)^{n}dx=16-6e\]
is
a) 2
b) 3
c) 4
d) 5

View Answer

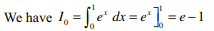
38. If \[I=\int_{0}^{\pi/2} \frac{\sin^{3}x\cos x}{\sin^{4}x+\cos^{4}x}dx\]
then I equals
a) \[\pi/8\]
b) \[\pi/4\]
c) \[\pi/2\]
d) \[\pi\]

View Answer

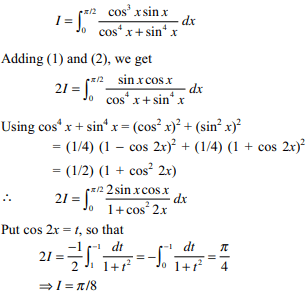
39. Let f : [0, 1] \[\rightarrow\]  R be a continuous function such that \[\int_{0}^{\pi} f\left(\sin x\right)dx=2018\]
then \[\int_{0}^{\pi}xf\left(\sin x\right)dx\]
is equal to
a) \[1009\pi\]
b) \[2016\pi\]
c) \[1008\pi\]
d) \[2017\pi\]

View Answer

40. For a > 0, let \[I\left(a\right)=\frac{3}{2}\int_{0}^{a} \frac{\sqrt{x\left(x^{2}+x+1\right)}}{\sqrt{x+1}\sqrt{x^{4}+x^{2}+1}}dx\]
then I (a) is equal to
a) \[ln \left(\sqrt{a+1}+\sqrt{a}\right)\]
b) \[ln \left(\sqrt{a^{2}+1}+a\right)\]
c) \[ln \left(\sqrt{a^{3}+1}+\sqrt{a^{3}}\right)\]
d) \[2ln \left(\sqrt{a^{2}+1}+a\right)\]

View Answer

41.If \[I=\int_{0}^{2\pi}e^{x/2}\sin\left(\frac{x}{2}+\frac{\pi}{4}\right)dx\]
then I equals
a) \[\pi\]
b) 0
c) \[-\pi/2\]
d) \[2\pi\]

View Answer

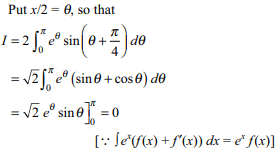
42. If \[I=\int_{0}^{2\pi}e^{x}\cos\left(\frac{x}{2}+\frac{\pi}{4}\right)dx\]
then I equals
a) \[\frac{-3}{5}\left(e^{2\pi}-1\right)\]
b) \[\frac{-3\sqrt{2}}{5}\left(e^{2\pi}-1\right)\]
c) \[\frac{-3\sqrt{2}}{5}\left(e^{2\pi}+1\right)\]
d) 0

View Answer

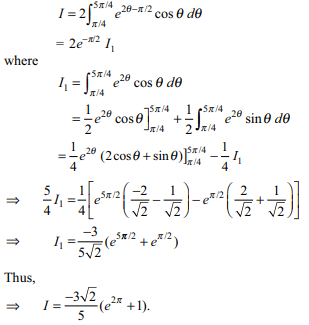
43.Let a, b, c, > 0 and b > c, If \[I=e^{a}\int_{b}^{c} \frac{x^{4}+1}{x^{6}+1}dx\]
then
a) \[I<\left(\frac{c}{b}\right)^{a}\]
b) \[I>e^{ab}\]
c) \[I< e^{ac}\]
d) \[I< e^{a\left(c-b\right)}\]

View Answer

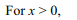
44. Let \[I=4\int_{0}^{\pi/4}\frac{x^{2}\left(\sin 2x-\cos 2x\right)}{\left(\sin x+\cos x\right)^{2}\cos^{2} x} dx\]
a) \[\frac{\pi^{2}}{4}-\pi\log\left(2\right)\]
b) \[\frac{\pi^{2}}{2}+\frac{1}{2}\pi\log\left(2\right)\]
c) \[\pi^{2}-\frac{3}{4}\pi\log\left(2\right)\]
d) \[\frac{\pi^{2}}{16}+\frac{1}{4}\pi\log\left(2\right)\]

View Answer

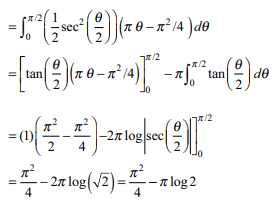
45. If \[I=\int_{\pi/3}^{2\pi/3} \frac{x}{1+\sin x}dx\]
then I equal to
a) \[2\pi\]
b) \[\left(2+\sqrt{3}\right)\pi\]
c) \[\left(2-\sqrt{3}\right)\pi\]
d) 0

View Answer

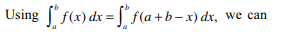
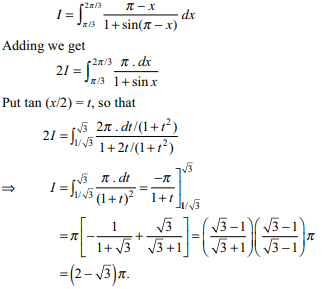
46. If \[I=\int_{\pi/6}^{\pi/3} \frac{dx}{1+\sqrt{\tan x} }dx\]
then I equals
a) \[\frac{\pi}{12}\]
b) \[\frac{\pi}{6}\]
c) \[\frac{\pi}{4}\]
d) \[\frac{\pi}{3}\]

View Answer

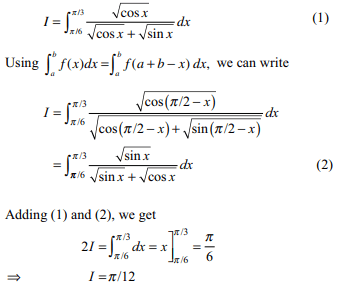
47. If \[I_{1}=\int_{0}^{\pi/1} f\left(\sin 2x\right)\sin x dx\]
and \[I_{2}=\int_{0}^{\pi/4} f\left(\cos 2x\right)\cos x dx\]
then \[\frac{I_{1}}{I_{2}}\]  equals
a) 1
b) \[1/\sqrt{2}\]
c) \[\sqrt{2}\]
d) 2

View Answer

48. If \[\int_{0}^{1}\frac{\sin t}{1+t}dt=\alpha\]
then value of \[I=\int_{4\pi-2}^{4\pi}\frac{\sin\left(x/2\right)}{4\pi+2-x}dx\]
is
a) \[\alpha/2\]
b) \[-\alpha\]
c) \[-\alpha/2\]
d) \[\alpha\]

View Answer

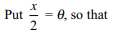
49. If \[I=\int_{-\pi}^{\pi}\frac{2x\left(1+\sin x\right)}{1+\cos^{2} x}dx\]
then I equals
a) \[-\sqrt{2}\pi^{2}\]
b) \[\pi^{2}\]
c) \[\frac{\pi^{2}}{\sqrt{2}}\]
d) \[-\frac{\pi^{2}}{\sqrt{2}}\]

View Answer

50. If \[h\left(x\right)=\int_{1}^{x} \sin^{4}t dt\]
then h(x + \[\pi\] ) equals
a) h(x) + h( \[\pi\] )
b) h(x) h( \[\pi\] )
c) h(x) - h( \[\pi\] )
d) h(x)/h( \[\pi\] )

View Answer

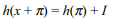
51. If \[I=\int_{0}^{1}\cot^{-1} \left(1-x+x^{2}\right)dx=k\int_{0}^{1}\tan^{-1} x dx \]
then k equals
a) 1
b) 2
c) \[\pi\]
d) \[2\pi\]

View Answer

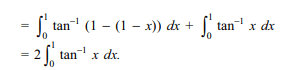
52. Let \[f:\left(0,\infty\right)\rightarrow\left(0,\infty\right)\]     be a differential
function satisfying \[x\int_{0}^{x} \left(1-t\right)f\left(t\right)dt=\int_{0}^{x} tf\left(t\right) dt,x>0\]
and f (1) = 1. The function f (x) is given by
a) \[\frac{1}{x^{3}}e^{1/x}\]
b) \[\frac{1}{x^{3}}e^{-1/x}\]
c) \[\frac{1}{x^{2}}e^{1-\frac{1}{x}}\]
d) \[\frac{1}{x^{3}}e^{1-\frac{1}{x}}\]

View Answer

53. Let f (x) = x – [x], where for x \[\epsilon\] R, [x] denotes the greatest integer \[\leq x\] . Then \[I=\int_{-2}^{2} f\left(x\right)dx\]     equals
a) -2
b) -1
c) 0
d) 2

View Answer

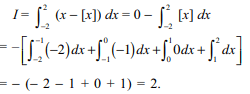
54. If n > 1, and \[I=\int_{0}^{\infty} \frac{dx}{\left(x+\sqrt{1+x^{2}}\right)^{n}}\]
then I equals
a) \[ \frac{n}{n^{2}-1}\]
b) \[ \frac{2n}{n^{2}-1}\]
c) \[ \frac{n}{2\left(n^{2}-1\right)}\]
d) \[\sqrt{n^{2}-1}\]

View Answer

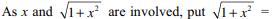
55. If [x] denotes the greatest integer \[\leq x\] and \[n\epsilon N\] , then value of \[I_{n}=\int_{0}^{n^{2}} \left[\sqrt{x}\right]dx\]
is
a) \[\frac{1}{6}\left(n-1\right)n\left(4n+1\right)\]
b) \[\frac{1}{6}\left(n-1\right)n^{2}\left(2n+1\right)\]
c) \[\frac{1}{6}\left(n-1\right)\left(n\right)\left(2n-1\right)\]
d) \[\frac{1}{6}\left(n-1\right)\left(3n+5\right)\]

View Answer

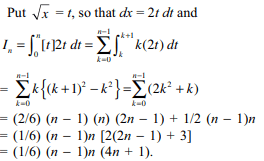
56. If \[I=\int_{0}^{1} \frac{dx}{\left(1+x\right)\left(2x+x\right)\sqrt{x\left(1-x\right)}}\]
then I equals
a) \[2\pi\]
b) \[\pi\]
c) \[\frac{\pi}{2}\]
d) \[\frac{\pi}{\sqrt{6}}\left(\sqrt{3}-1\right)\]

View Answer

57. For a > 0, \[f\left(t\right)=\int_{0}^{\pi}\left(ax-t\sin x\right) ^{2}dx\]
\[\min_{0\leq t\leq 1} f\left(t\right)\]     is
a) \[\frac{a\pi^{3}}{3}-\frac{1}{2}\pi a^{2}\]
b) \[\frac{a\pi^{3}}{3}-\frac{3}{2}\pi a^{2}\]
c) \[\frac{a\pi^{3}}{3}+\frac{1}{2}\pi a^{2}\]
d) \[\frac{a\pi^{3}}{3}-\pi a^{2}\]

View Answer

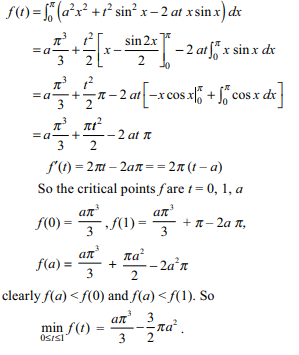
58. If \[I=\int_{-1}^{2}\mid x\sin\pi x \mid dx\]
then I equals
a) \[1/\pi\]
b) \[2/\pi\]
c) \[4/\pi\]
d) \[5/\pi\]

View Answer

59. Let \[I=\int_{0}^{\pi}\mid \sin x+\sin 2x +\sin 3x\mid dx\]
then
a) 6I = 5
b) 6I = 11
c) 6I = 17
d) 6I = 19

View Answer

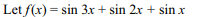
60. If \[I=\int_{\alpha}^{\beta}\left[\log \log x+\frac{1}{\left(\log x\right)^{2}}\right] dx\]
then I equals
a) \[\alpha\log \log\alpha-\beta\log\log\beta\]
b) \[\frac{1}{\alpha}-\frac{1}{\beta}+\log\log\alpha-\log\log\beta\]
c) \[\frac{\beta-\alpha}{\alpha\beta}+\alpha\log\log\alpha-\beta\log\log\beta\]
d) \[\beta \log\log\beta-\alpha\log\left(\log\alpha\right)-\frac{\beta}{\log\beta}+\frac{\alpha}{\log\alpha}\]

View Answer

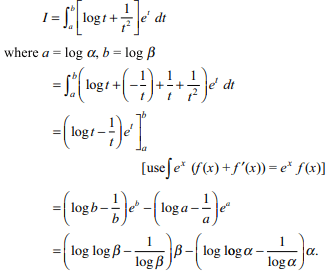
61.If \[I=\int_{0}^{\pi/4} \frac{\sin 2\theta}{\sin^{2}\theta+\cos^{4}\theta}d\theta\]
then I equals
a) \[\pi/2\]
b) \[\pi/\sqrt{3}\]
c) \[\pi/2\sqrt{3}\]
d) \[\pi/3\sqrt{3}\]

View Answer

62. Let \[u\left(x\right)=\log\left(x+\sqrt{1+x^{2}}\right),x\epsilon R\]
and \[f\left(x\right)=\frac{\left(1-x+x^{2}\right)\cos u\left(x\right)-\sqrt{1+x^{2}}\sin u\left(x\right)}{\left(1+x^{2}\right)^{3/2}},x\epsilon R\]
then \[\int_{0}^{1} f\left(x\right)dx\]     is equal to
a) \[\sin \left(u\left(1\right)\right)+\cos \left(u\left(1\right)\right)-1\]
b) \[\sin \left(u\left(1\right)\right)+\frac{1}{\sqrt{2}}\cos \left(u\left(1\right)\right)-1\]
c) \[\frac{1}{\sqrt{2}}\sin \left(u\left(1\right)\right)+\cos \left(u\left(1\right)\right)-1\]
d) \[\frac{1}{\sqrt{2}}\left[\sin \left(u\left(1\right)\right)+\cos \left(u\left(1\right)\right)-1\right]\]

View Answer

63.If \[I=\int_{8}^{15}\frac{dx}{\left(x-3\right)\sqrt{x+1}}\]
then I equals
a) \[\frac{1}{2}\log\frac{5}{3}\]
b) \[2\log\frac{1}{3}\]
c) \[\frac{1}{2}\log\frac{1}{5}\]
d) \[2\log\frac{5}{3}\]

View Answer

64. If \[I=\int_{1}^{\infty}\frac{dx}{x^{2}\sqrt{1+x}}\]
then I equals
a) \[\sqrt{2}+\log(\sqrt{2}-1)\]
b) \[\sqrt{2}-\log(\sqrt{2}-1)\]
c) \[\log(\sqrt{2}+1)-\sqrt{2}\]
d) \[\sqrt{2}+\log(3-\sqrt{2})\]

View Answer

65. \[\lim_{x \rightarrow \pi/4}\frac{\int_{2}^{\sec^{2} x}f\left(t\right)dt }{x^{2}-\pi^{2}/16}\]     equals
a) \[\frac{8}{\pi}f\left(2\right)\]
b) \[\frac{2}{\pi}f\left(2\right)\]
c) \[\frac{2}{\pi}f\left(\frac{1}{2}\right)\]
d) 4 f (2)

View Answer

66. The area of the region between the curves \[y=\sqrt{\frac{1+\sin x}{\cos x}}\]     and \[y=\sqrt{\frac{1-\sin x}{\cos x}}\]
bounded by the lines x = 0 and \[x=\frac{\pi}{4}\]
is
a) \[\int_{0}^{\sqrt{2}-1} \frac{t}{\left(1+t^{2}\right)\sqrt{1-t^{2}}}dt\]
b) \[\int_{0}^{\sqrt{2}-1} \frac{4t}{\left(1+t^{2}\right)\sqrt{1-t^{2}}}dt\]
c) \[\int_{0}^{\sqrt{2}+1} \frac{4t}{\left(1+t^{2}\right)\sqrt{1-t^{2}}}dt\]
d) \[\int_{0}^{\sqrt{2}+1} \frac{t}{\left(1+t^{2}\right)\sqrt{1-t^{2}}}dt\]

View Answer

67. For \[k\epsilon N\] , Let \[a_{k}=\int_{0}^{1} \frac{x\sin \pi x}{x+\left(1-x\right)k^{1-2x}}dx\]
a) \[a_{k}\] is independent of k
b) \[\lim_{n \rightarrow \infty}\left(\frac{1}{n}\sum_{k=1}^na_{k}\right)=\pi\]
c) \[a_{1},a_{2},a_{3}....\]     an A.P
d) All of the Above

View Answer

68. For \[k\epsilon N\] ,Let \[b_{k}=\int_{1}^{e} \frac{1}{\left(k+\log x\right)\left(k+1+\log x\right)}\frac{dx}{x}\]
and \[a_{n}=\sum_{k=1}^n b_{k}\]
then
a) \[b_{k}=\log\left(\frac{\left(k+1\right)^{2}}{k\left(k+2\right)}\right)\]
b) \[a_{n}=\log\left(\frac{2n+2}{n+2}\right)\]
c) \[\lim_{n \rightarrow \infty}a_{n}=\log2\]
d) All of the Above

View Answer

69. a, \[b\epsilon R\] , \[\mid a\mid \leq 1,\mid b\mid \leq 1,\]
let \[I \left(a,b\right)=\int_{0}^{\pi} \left(a\sin x+b\cos x\right)^{3}dx\]
then
a) I (a, b) is independent of a
b) minimum value of I (–1, b) is \[\frac{-10}{3}\]
c) Maximum value of I (a, 1) is \[\frac{10}{3}\]
d) Both b and c

View Answer

70. For \[n\epsilon N\] , n > 2, let \[I_{n}=\int_{0}^{1} \frac{dx}{\left(1+x^{n}\right)^{1+1/n}}dx\]
then
a) \[\left(I_{n}\right)^{n}=\frac{1}{2}\]
b) \[\lim_{n \rightarrow \infty}I_{n}=1\]
c) \[\lim_{n \rightarrow \infty}I_{n}=ln 2\]
d) Both a and b

View Answer

71.For a > 0, let \[I\left(a\right)=\int_{0}^{a} \frac{dx}{1+e^{a^{2}-2ax}}\]
and let \[0<\theta<\pi/2\]    , then
a) \[I'\left(a\right)=ln \sqrt{e}\]
b) \[I\left(\sin\theta\right)+I \left(\cos\theta\right) \leq\sin \left(\pi/4\right)\]
c) \[I\left(\sin^{2}\theta\right)+I \left(\cos^{2}\theta\right) =\frac{1}{2}\]
d) All of the Above

View Answer

72. Let \[I=\int_{-1}^{1} \left(\frac{1+2018^{\mid x\mid}}{1+2017^{x}}+\frac{1+2017^{\mid x\mid}}{1+2018^{x}}\right)dx\]
equals
a) I > 2
b) I < 4017
c) I > 4
d) All of the Above

View Answer

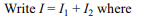
73.The value of the integral \[I=\int_{0}^{\pi/4}\frac{dx}{a\cos ^{2} x+b\sin^{2} x}\]
is
a) \[\frac{1}{\sqrt{ab}}\tan^{-1}\sqrt{\frac{b}{a}}\left(a>0,b>0\right)\]
b) \[\frac{1}{\sqrt{ab}}\tan^{-1}\sqrt{\frac{b}{a}}\left(a<0,b<0\right)\]
c) \[\frac{\pi}{4a}\left(a=b\right)\]
d) All of the Above

View Answer

74. If \[I_{1}=\int_{1}^{\pi} \frac{dx}{e^{3x}+\sin^{3} x}\]
and \[I_{2}=\int_{1}^{\pi} \frac{dx}{\left(e^{x}+\sin x\right)^{3}}\]     then
a) \[I_{1}\leq4I_{2}\]
b) \[I_{1}>I_{2}\]
c) \[I_{1}\leq6I_{2}\]
d) All of the Above

View Answer

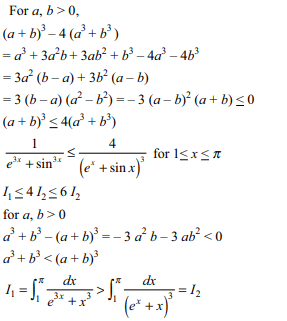
75. For 0 < t < 1, let \[F_{n}\left(t\right)=\frac{1}{2t} \int_{0}^{1} \mid x^{n}-t\mid dx+\frac{1}{2}\]
and let \[a_{n}\] be the least value of \[F_{n}\left(t\right)\] for 0 < t < 1, then
a) \[F_{n}\left(t\right)=\frac{1}{\left(n+1\right)}\left[\frac{1}{t}+2nt^{1/n}\right]\]
b) \[a_{n}=2^{-1/\left(n+1\right)}\]
c) \[\lim_{n \rightarrow \infty}a_{n}a_{n+1}....a_{2n-1}=2^{-\log 2}\]
d) All of the Above

View Answer

76. For \[a\geq 1\] , let \[I\left(a\right)=\int_{-1/a}^{1/a} \left(2x^{6}+2x^{4}+3\right)\cos^{-1}\left(ax\right)dx\]
then
a) \[I\left(a\right)\leq\frac{129\pi}{35 a}\]
b)\[I\left(a\right)=\pi\left(\frac{2}{7a^{7}}+\frac{2}{5a^{5}}+\frac{3}{a}\right)\]
c) I(a) is independent of a
d) Both a and b

View Answer

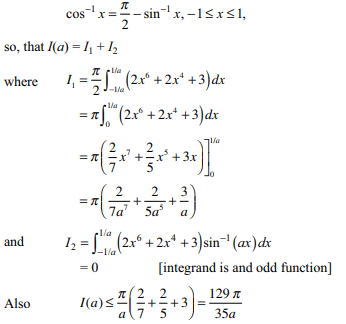
77. Let f be a real value function such that \[f\left(\frac{1}{x}\right)=f\left(x\right)\forall x\neq0\]
Let a > 0 and \[I=\int_{\sqrt{2}-1}^{\sqrt{2}+1} \frac{dx}{\left(1+x^{2}\right)\left(1+a^{f\left(x\right)}\right)}\]
a) independent of a
b) independent of function f
c) \[\tan^{-1}\left(\sqrt{2}+1\right)-I=\pi/4\]
d) All of the Above

View Answer

78. Let \[a\epsilon \left(0,\pi/2\right)\] , b \[\geq\] 1, m, \[n\epsilon N\] and let f, g, h, k: [–a, a] \[\rightarrow R\]
be four continuous functions such that f(–x) = –f(x), g(–x) = –g(x), h(–x) = h(x), k(–x) = k(x), and let \[I=\int_{-a}^{a}\frac{f\left(x\right)+g\left(x\right)}{\left(b-\cos x\right)^{m}h\left(x\right)+k\left(x\right)\sin^{2n}x}dx\]
a) I is independent of a
b) I is independent of f and g
c) I is independent of h and k
d) All of the Above

View Answer

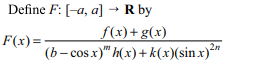
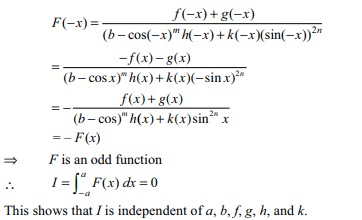
79. Let \[f\left(x\right)=\frac{\sin x-2\log\left(\frac{1-\sin x}{\cos x}\right)}{\left(1+\cos2x\right)\sqrt{\log\left(\frac{1+\sin x}{\cos x}\right)}},0\leq x\leq\frac{\pi}{4}\]
and \[I=\int_{0}^{\pi/4} f\left(x\right)dx\]     then
a) \[I=\log\left(\sqrt{2}+1\right)\]
b) \[I=\sqrt{\log\left(\sqrt{2}+1\right)}\]
c) \[I=\sqrt{\log\cot\left(\pi/8\right)}\]
d) Both b and c

View Answer

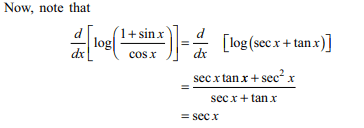
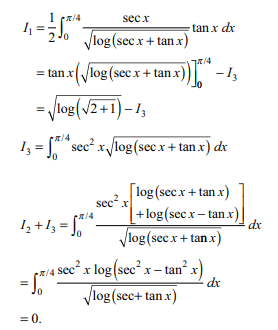
80. If \[I=\int_{-\pi}^{\pi} \frac{dx}{2-\sin x}\]
then I is equal to
a) \[\frac{2\pi}{3}\]
b) \[\frac{2\pi}{\sqrt{3}}\]
c) \[\frac{\pi}{\sqrt{3}}\]
d) \[\frac{\pi}{3}\]

View Answer