PrepBharat

1. If \[I=\int\frac{dx}{\left( 1+x^{4}\right)^{1/4}}\]
then I is equals
a) \[\frac{1}{2}\tan^{-1}\left(\frac{x}{\left(1+x^{4}\right)^{1/4}}\right)+C\]
b) \[\frac{1}{4}\log\mid\frac{1-\left(1+x^{4}\right)^{1/4}}{1+\left(1+x^{4}\right)^{1/4}}\mid+C\]
c) \[\frac{1}{2}\tan^{-1}\left(\frac{\left(1+x^{4}\right)^{1/4}}{x}\right)-\frac{1}{4}\log\left(\frac{1-\left(1+x^{4}\right)^{1/4}}{1+\left(1+x^{4}\right)^{1/4}}\right)+C\]
d) \[\frac{1}{2}\tan^{-1}\left(\frac{\left(1+x^{4}\right)^{1/4}}{x}\right)-\frac{1}{4}\log\left(\frac{x-\left(1+x^{4}\right)^{1/4}}{x+\left(1+x^{4}\right)^{1/4}}\right)+C\]

View Answer

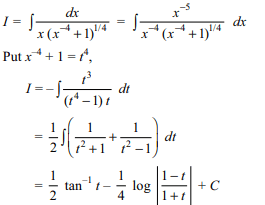
2. If \[I=\int\tan^{-1}\left(1+\sqrt{x}\right)dx\]
then I is equals
a) \[x ^{2}\tan^{-1}\left(1+\sqrt{x}\right)-\sqrt{x}+\log\left(x+2\sqrt{x}+2\right)+C\]
b) \[\left(2\sqrt{2}+1\right)\tan^{-1}\left(1+\sqrt{x}\right)+\sqrt{x}-\log\left(x+2\sqrt{x}+2\right)+C\]
c) \[\left(\sqrt{x-1}\right)^{2}\tan^{-1}\left(1+\sqrt{x}\right)-\sqrt{x}+\log\left(\sqrt{x}+1\right)+C\]
d) none of these

View Answer

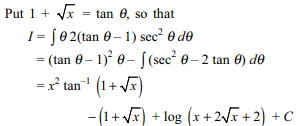
3. If \[I=\int\frac{2x+3}{\left(x^{2}+2x+3\right)\sqrt{x^{2}+2x+4}}dx\]
then I is equals
a) \[ \log\mid\frac{\sqrt{x^{2}+2x+4}-1}{\sqrt{x^{2}+2x+4}+1}\mid+C\]
b) \[ \log\mid\frac{\sqrt{x^{2}+2x+4}-1}{\sqrt{x^{2}+2x+4}+1}\mid+\tan^{-1}\left(\frac{x+2}{3}\right)+C\]
c) \[ \log\tan^{-1}\left(\frac{\sqrt{x+3}}{2}\right)+C\]
d) none of these

View Answer

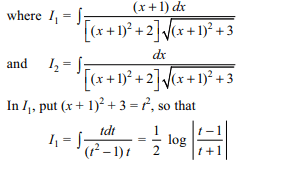
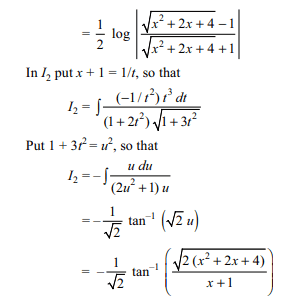
4. If \[I=\int\cot^{-1}\left(\frac{a^{2}-ax+x^{2}}{a^{2}}\right)dx\]
then I is equals
a) \[x \tan^{-1}\left(\frac{x}{a}\right)-\left(x-a\right)\tan^{-1}\left(\frac{x-a}{a}\right)+C\]
b) \[\frac{a}{2}\log\left(2a^{2}-2ax+x^{2}\right)-\frac{a}{2}\log\left(x^{2}+a^{2}\right)+C\]
c) \[x \tan^{-1}\left(\frac{x}{a}\right)+\left(x-a\right)\tan^{-1}\left(\frac{x-a}{a}\right)+\frac{a}{2}\log\left(2a^{2}-2ax+x^{2}\right)+C\]
d) \[\tan^{-1}\left(\frac{x}{a}\right)+x\tan^{-1}\frac{x-a}{a}+\log\left(2a^{2}-2ax+x^{2}\right)+C\]

View Answer

5. If \[I=\int\frac{\cos x}{\sin ^{3}x-\cos^{3} x}dx\]
and \[f\left(x\right)=\frac{1}{3}\log\left(\tan x-1\right)+\frac{1}{\sqrt{3}}\tan^{-1}\left(\frac{2\tan x+1}{\sqrt{3}}\right),g\left(x\right)=\frac{1}{6}\log\left(\tan^{2}x+\tan x+1\right)\]
then I is equals
a) f(x) – g(x) + C
b) f(x) g(x) + C
c) f(x)/g(x) + C
d) f(x) + g(x) + C

View Answer

6. If \[I=\int\frac{\sqrt{\sin^{3}2x}}{\sin^{5}x}dx\]
and \[f\left(x\right)=\left(\cot x\right)^{3/2},g\left(x\right)=\left(\cot x\right)^{5/2}\]
then I is equals
a) \[\left(2\sqrt{3}/3\right) f\left(x\right) -\left(1/5\right) g\left(x\right)+C\]
b) \[-\left(4\sqrt{2}/5\right)g\left(x\right) +C\]
c) \[\left(1/2\sqrt{3}\right)f\left(x\right) +C\]
d) \[\left(2\sqrt{2}/3\right)f\left(x\right)+ 1/5f\left(x\right)+C\]

View Answer

7. If \[\int\frac{dx}{\left(x^{2}+1\right)\left(x^{2}+4\right)}=K\tan^{-1}x+L\tan^{-1}\frac{x}{2}+C\]
then
a) K = 1/3
b) L = 2/3
c) L = – 1/6
d) Both a and c

View Answer

8. If \[\int\frac{\cos^{4}x}{\sin^{2}x}dx=K\cot x+M\sin 2x+L\frac{x}{2}+C\]
then
a) L = – 3
b) K = – 2
c) M = – 1/4
d) Both a and c

View Answer

9. If \[\int\frac{3x+4}{x^{3}-2x-4}dx=\log\mid x-2\mid+K\log f\left(x\right)+C\]
then
a) K = – 1/2
b) \[f\left(x\right)= x^{2}+2x+2 \]
c) \[f\left(x\right)=\mid x^{2}+2x+2 \mid\]
d) All of the Above

View Answer

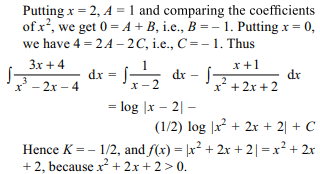
10. If \[\int\frac{dx}{5+4\cos x}=K\tan^{-1}\left(M\tan\frac{x}{2}\right)+C\]
then
a) K = 1
b) K = 2/3
c) M = 1/3
d) Both b and c

View Answer

11.Let \[I=\int_{0}^{1} \] (x + 1) (x + 2) (x + 3) (x + 4) (x + 5) dx, then
a) I > 400
b) I > 700
c) I < 300
d) I < 200

View Answer

12. If \[I=\int_{1}^{2} x^{-x}dx\]
then
a) \[I<\frac{3}{4}\]
b) \[I\geq\frac{3}{4}\]
c) I>1
d) I>2

View Answer

13. If \[I=\int_{1/3}^{3} \sin^{11}\left(x-\frac{1}{x}\right)\frac{dx}{x}\]
then I is equal to
a) 0
b) sin 3 – sin (1/3)
c) \[\frac{1}{12}\left(\sin3-\sin\left(1/3\right)\right)^{5}\]
d) \[\frac{1}{6}\left(\sin3-\sin 1/3\right)^{4}\]

View Answer

14. If \[I=\int_{0}^{\infty} \frac{\tan^{-1}x}{x^{2}+x+1}dx\]
then I is equal to
a) \[\frac{\pi^{2}}{4\sqrt{3}}\]
b) \[\frac{\pi^{2}}{6\sqrt{3}}\]
c) \[\frac{\pi^{2}}{4}\]
d) \[\frac{\pi^{2}}{2\sqrt{2}}\]

View Answer

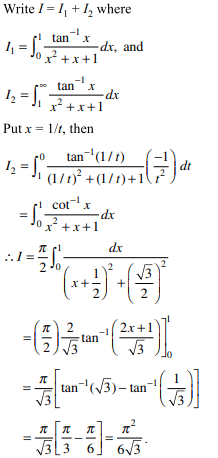
15. If \[I=\int_{0}^{\pi/4}\frac{\sin4x }{\sqrt{1+\sin^{2}x}}dx\]
then I is equal to
a) \[8\sqrt{\frac{3}{2}}\]
b) \[\frac{28}{3}-\frac{\pi}{3}\]
c) \[8\sqrt{\frac{3}{2}}-\frac{28}{3}\]
d) \[\frac{\pi^{2}}{16}\]

View Answer

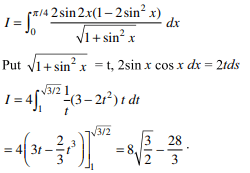
16. If \[I=\int_{-\pi/2}^{\pi/2}\frac{\sqrt{\cos^{2}x+\cos^{4}x }}{5^{x}+1}dx\]
then I is equal to
a) \[\frac{1}{4}ln5+\frac{\pi}{6}\]
b) \[\frac{1}{2}ln5+\frac{\pi}{6}\]
c) \[\frac{1}{2}+\frac{\pi}{6}\]
d) \[\frac{3}{2}+\frac{\pi}{6}\]

View Answer

17. If \[I=\int_{0}^{2016}x\left(x-4\right)\left(x-8\right)\left(x-12\right)....\left(x-2016\right)dx\]
then I is equal to
a) 2016
b) 1008
c) 0
d) \[\left(10008\right)^{2}\]

View Answer

18. If \[f(x)=\int_{1}^{x}\left(\frac{1}{x}-\frac{1}{t}\right)f'\left(t\right)dt+\frac{1}{x},x>0\]
then f (x) is equal to
a) \[e^{1/x-1}\]
b) \[e^{x-1}\]
c) \[x e^{x-1}\]
d) \[x e^{1/x-1}\]

View Answer

19. The equation of the tangent to the curve \[y=\int_{x}^{x^{2}}\] log t dt   at x=2 is
a) y – 6 log 2 = 7 log 2(x – 2)
b) \[y-\log 2e^{1/3}=\left(\log 2\right)x\]
c) \[y-8\log 2e^{-1/3}=5 \log 2x\]
d) y + 9 log 2 + 2 = (7 log 2)x.

View Answer

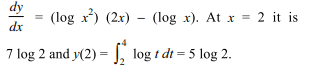
20. The value of\[\int_{-1}^{1}x \mid x \mid\]  dx is
a) 2
b) 1
c) 0
d) none of these

View Answer

21. The value of \[\int_{-\pi/2}^{\pi/2}\log \left(\frac{2-\sin\theta}{2+\sin\theta}\right)d\theta\]
is
a) 0
b) 1
c) 2
d) none of these

View Answer

22. The area bounded by \[y=x^{2}\]  and \[y=1-x^{2}\]
is
a) \[\sqrt{8}/3\]
b) 16/3
c) 32/3
d) 2

View Answer

23. The value of the integral \[\int_{0}^{\pi^{2}/4}\sin \sqrt{x} dx\]
is
a) 1
b) 1/2
c) 3/2
d) 2

View Answer

24. The difference between the greatest and least values of the function \[f\left(x\right)=\int_{0}^{x}\left(t+1\right) dt\]
on [2, 3] is
a) 3
b) 2
c) 7/2
d) 11/2

View Answer

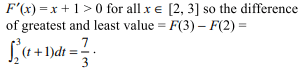
25. The area of the figure bounded by the lines x = 0 , \[x=\pi/2\]  , \[f\left(x\right)=\sin x\]    and \[g\left(x\right)=\cos x\]    is
a) \[2\left(\sqrt{2}-1\right)\]
b) \[\sqrt{3}-1\]
c) \[2\left(\sqrt{3}-1\right)\]
d) \[2\left(\sqrt{2}+1\right)\]

View Answer

26. The value of \[\lim_{x \rightarrow \infty}\frac{\int_{0}^{x}e^{2x}dx}{\int_{0}^{x}e^{2x^{2}}dx}\]
is
a) 1
b) 2
c) 3
d) 0

View Answer

27. The value of the integral \[\int_{0}^{3}\frac{dx}{\sqrt{x+1}+\sqrt{5x+1}}\]
is
a) 11/15
b) 14/15
c) 2/5
d) \[\frac{1}{2}\left(1+\frac{1}{2}\log2\right)\]

View Answer

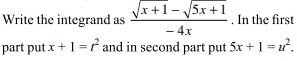
28. The value of the integral \[\int_{0}^{\pi/4}\frac{\sin x+\cos x}{3+\sin 2x}dx\]
is
a) log 2
b) log 3
c) (1/4) log 3
d) (1/9) log 3.

View Answer

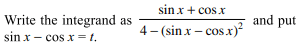
29. The area of the figure bounded by \[y^{2}=2x+1\]    and x – y – 1 = 0 is
a) 2/3
b) 4/3
c) 8/3
d) 11/3

View Answer

30. A polynomial P is positive for x > 0 and the area of the region bounded by P(x), the x-axis, and the vertical lines x = 0 and x = k is \[k^{2}\left(k+3\right)/3.\]
The polynomial P(x) is
a) \[x^{2}+x+1\]
b) \[x^{2}+2x+1\]
c) \[x^{2}+2x\]
d) \[x^{3}+1\]

View Answer

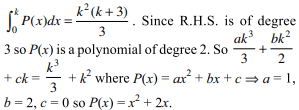
31.If \[I=\int_{1}^{2} \frac{dx}{\left(x+1\right)\sqrt{x^{2}-1}}\]
then I is equal to
a) 1
b) 2
c) \[1/\sqrt{2}\]
d) \[1/\sqrt{3}\]

View Answer

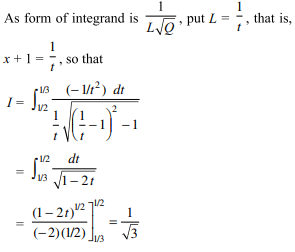
32. \[\lim_{x \rightarrow 0} \frac{\int_{0}^{x}\sin t^{2}dt}{\sin x^{2}}\]
is
a) 1
b) 0
c) 2
d) 3/2

View Answer

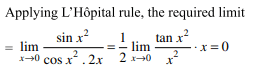
33. The value of \[\int_{-2}^{2}\mid 1-x\mid dx\]
is
a) 2
b) 0
c) 4
d) 5

View Answer

34.If \[f\left(x\right)=\int_{0}^{x}\cos^{4}t dt\]
then \[f\left(x+\pi\right)\]    equals
a) \[\frac{f\left(x\right)}{f\left(\pi\right)}\]
b) \[{f\left(x\right)}{f\left(\pi\right)}\]
c) \[{f\left(x\right)}+{f\left(\pi\right)}\]
d) \[{f\left(x\right)}-{f\left(\pi\right)}\]

View Answer

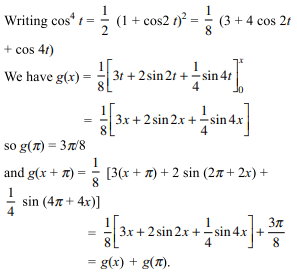
35. Suppose that the graph of y = f (x) contains the point (0, 4) and (2, 7). If f' is continuous then \[\int_{0}^{2}f'\left(x\right) dx\]    is equal to
a) 2
b) -2
c) 3
d) none of these

View Answer

36. If a continuous function f satisfies \[\int_{0}^{f\left(x\right)}t^{2} dt =x^{2}\left(1+x\right)\]
for all x ≥ 0 then f (2) is equal to
a) 12
b) \[\sqrt[3]{36}\]
c) 3
d) \[\sqrt[3]{42}\]

View Answer

37. If a continuous function f satisfies \[\int_{0}^{x^{2}}f\left(t\right) dt =x^{2}\left(1+x\right)\]
then f (4) is equal to
a) 7
b) 4
c) 5
d) 6

View Answer

38. If \[m\neq n,m,n\epsilon N\]   , then the value of \[\int_{0}^{2\pi}\cos mx \cos nx dx\]
is
a) 0
b) \[2\pi\]
c) \[\pi\]
d) dependent on m and n

View Answer

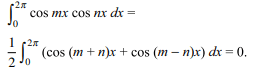
39. The value of\[\int_{0}^{\sin^{2} x}\sin^{-1}\sqrt{t} dt+\int_{0}^{\cos^{2} x}\cos^{-1}\sqrt{t}dt\]
is
a) 0
b) \[\pi/4\]
c) \[\pi/2\]
d) \[\pi/3\]

View Answer

40. The value of\[\int_{1/e^{2}}^{e} \mid \log x\mid dx\]
is
a) \[2\left(1-1/e^{2}\right)\]
b) \[2-3/e^{2}\]
c) \[1-2/e^{2}\]
d) \[3-2/e^{2}\]

View Answer

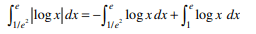
41.If \[I=\int_{0}^{1/\sqrt{3}} \frac{dx}{\left(1+x^{2}\right)\sqrt{1-x^{2}}}\]
then I is equal to
a) \[\pi/2\]
b) \[\pi/2\sqrt{2}\]
c) \[\pi/4\sqrt{2}\]
d) \[\pi/4\]

View Answer

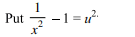
42. Let f be a continuous function on R satisfying f (x + y) = f (x) + f (y) for all x, \[y\epsilon R\]  with f (1) = 2 and g be a function satisfying \[f\left(x\right)+g\left(x\right)=e^{x}\]     then the value of the integral \[\int_{0}^{1} f\left(x\right)g\left(x\right)dx\]     is
a) 1/e – 4
b) \[\frac{1}{4}(e – 2)\]
c) 2/3
d) (1/2) (e – 3)

View Answer

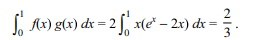
43. A line tangent to the graph of the function y = f (x) at the point x = a forms an angle \[\pi/3\]  with y-axis and at x = b and angle \[\pi/4\]  with x-axis then \[\int_{a}^{b} f''\left(x\right)dx\]    is
a) \[1/\sqrt{3}-1\]
b) \[\pi/12\]
c) \[-\pi/12\]
d) \[\sqrt{3}-1\]

View Answer

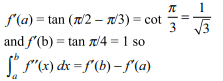
44. The value of \[\int_{1}^{e} \left(\frac{\tan^{-1}x}{x}+\frac{\log x}{1+x^{2}}\right)dx\]
is
a) tan e
b) \[\tan^{-1}e\]
c) \[\tan^{-1}(1/e)\]
d) \[2\tan^{-1}e\]

View Answer

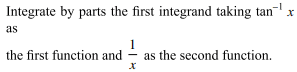
45. If a continuous function f on [0, a] satisfy f (x) f (a – x) = 1, a > 0 then \[\int_{0}^{a}\frac{dx}{1+f\left(x\right)}\]
is equal to
a) 0
b) a
c) a/2
d) none of these

View Answer

46. Let f (x), g(x) and h(x) be continuous function on [0, a] such that f (x) = f (a – x), g(x) = – g(a – x), 3h(x) – 4h(a – x) = 5 then \[\int_{0}^{a}\] f(x) g(x) h(x) dx is equal to
a) 1
b) 0
c) a
d) -1

View Answer

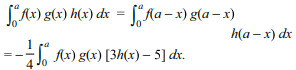
47. The value of \[\int_{0}^{\pi}\frac{dx}{1-2\alpha \cos x+\alpha^{2}}\]
is
a) \[\frac{\pi}{1+\alpha^{2}} if a>1\]
b) \[\frac{\pi}{\alpha^{2}-1} if a>1\]
c) \[\frac{\pi}{1+\alpha^{2}} if a<1\]
d) \[\frac{\pi}{\alpha^{2}-1} if a<1\]

View Answer

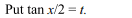
48. The value of \[\int_{0}^{1} \mid \sin 2\pi x\mid dx\]
is equal to
a) 0
b) \[-1/\pi\]
c) \[1/\pi\]
d) \[2/\pi\]

View Answer

49. Let f (x) and g(x) be two functions satisfying \[f\left(x^{2}\right)+g\left(4-x\right)=4x^{3},g\left(4-x\right)+g\left(x\right)=0,\]
then the value of \[\int_{-4}^{4} f\left(x^{2}\right)dx\]    is
a) 512
b) 64
c) 256
d) 0

View Answer

50. If \[f\left(x\right)=\int_{1}^{x} \frac{\log t}{t+1}dt\]      and \[f\left(x\right)+f\left(1/x\right)=k\left(\log x\right)^{2},\]
then k equal to
a) 1
b) 1/2
c) 1/4
d) 1/3

View Answer

51.If \[x=\int_{c^{2}}^{\tan t} \tan^{-1} z dz ,y=\int_{n}^{\sqrt{t}} \frac{\cos\left(z^{2}\right)}{z}dz\]
than \[\frac{dy}{dx}\] is equal to
a) \[\frac{\tan t}{2 t}\]
b) \[\frac{\cos^{2} t}{ t^{2}}\]
c) \[\frac{\cos^{3} t}{ 2t^{2}}\]
d) \[\frac{\tan t^{2}}{ 2t^{2}}\]

View Answer

52.If \[\int_{\log 2}^{x} \frac{dx}{\sqrt{e^{x}-1}}=\frac{\pi}{6}\]
the value of x is
a) 4
b) \[\log 2\]
c) \[\log 4\]
d) \[\log 8\]

View Answer

53.If \[I=\int_{1/ 2}^{1} \frac{dx}{x^{4}\sqrt{1-x^{2}}}\]
then I is equal to
a) 2
b) 2/3
c) \[2/\sqrt{3}\]
d) \[\sqrt{3}\]

View Answer

54. The value of \[\int_{-4}^{-5} e^{\left(x+5\right)^{2}}dx+3\int_{1/3}^{2/3} e^{9\left(x-2/3\right)^{2}}dx\]
is
a) 2/5
b) 1/5
c) 1/2
d) none of these

View Answer

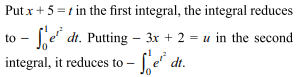
55. If \[f\left(x\right)= A\sin \left(\pi x/2\right)+B,f'\left(1/2\right)=\sqrt{2}\]
and \[\int_{0}^{1}f\left(x\right) dx= \frac{2A}{\pi}\]     , then the constants A and B are (resp.)
a) \[\pi/2,\pi/2\]
b) \[2/\pi,3\pi\]
c) \[0,-4\pi\]
d) \[4/\pi,0\]

View Answer

56.\[\int_{\pi/2}^{3\pi/2}\] [2 sin x] dx is equal to ([x] denotes the greatest integer function)
a) \[-\pi\]
b) 0
c) \[-\pi/2\]
d) \[\pi/2\]

View Answer

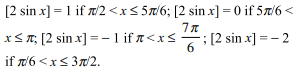
57. If \[f\left(x\right)=\begin{cases}e^{\cos x}\sin x & for\mid x \mid \leq 2\\2 & other wise \end{cases}\]
then \[\int_{-2}^{3}f\left(x\right) dx\]    is equal to
a) 0
b) 1
c) 2
d) 3

View Answer

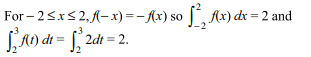
58. The value of \[\int_{e^{-1}}^{e^{2}}\mid\frac{\log x}{x} \mid dx\]     is
a) 3/2
b) 5/2
c) 3
d) 5

View Answer

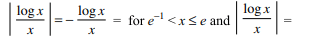
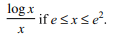
59. The value of\[\int_{-\pi}^{\pi}\frac{\cos^{2} x}{1+a^{x}} dx ,a>0\]     is
a) \[\pi/2\]
b) \[a\pi\]
c) \[\pi\]
d) \[2\pi\]

View Answer

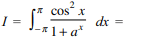
60. The integral \[\int_{-1/2}^{1/2}\left(\left[x\right]+\log\frac{1+x}{1-x}\right)dx\]
equals
a) -1/2
b) 0
c) 1
d) -2 log 2

View Answer

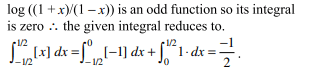
61.If \[0<\alpha<\pi/2\]    then the value of \[\int_{0}^{\alpha}\frac{dx}{1-\cos x\cos\alpha}\]
is
a) \[\pi/\alpha\]
b) \[\pi/\sin\alpha\]
c) \[\pi/\cos\alpha\]
d) \[\pi/2\alpha\]

View Answer

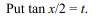
62. If \[I_{1}=\int_{x}^{1}\frac{dt}{1+t^{2}}\]     and \[I_{2}=\int_{1}^{1/x}\frac{dt}{1+t^{2}}\]
for x>0, then
a) \[I_{1}=I_{2}\]
b) \[I_{1}>I_{2}\]
c) \[I_{2}>I_{1}\]
d) \[I_{2}=\left(\pi/2\right)-\tan^{-1}x\]

View Answer

63. The solution of the equation \[\int_{\sqrt{2}}^{x}\frac{dx}{x\sqrt{x^{2}-1}}=\frac{\pi}{12}\]
is given by
a) 1
b) 2
c) 3
d) \[\sqrt{3}\]

View Answer

64. The mean value of the function \[f\left(x\right)=\frac{2}{e^{x}+1}\]
on the interval [0, 2] is
a) \[\log\frac{2}{e^{2}+1}\]
b) \[1+log\frac{2}{e^{2}+1}\]
c) \[2+\log\frac{2}{e^{2}+1}\]
d) \[2+\log\left(e^{2}+1\right)\]

View Answer

65. If \[I_{1}=\int_{x}^{1} \frac{dt}{1+t^{2}}\]     and \[I_{2}=\int_{1}^{1/x} \frac{dt}{1+t^{2}}\]     for x > 0 then
a) \[I_{1}=I_{2}\]
b) \[I_{1}>I_{2}\]
c) \[I_{2}=\left(\pi/4\right)-\tan^{-1}x\]
d) Both a and c

View Answer

66. The points of extremum of \[f\left(x\right)=\int_{1}^{x}e^{-t^{2}/2}\left(1-t^{2}\right)dt\]
are
a) x = 1
b) x = -1
c) x = 2
d) Both a and b

View Answer

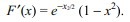
67. Let \[f\left(x\right)=\int_{x^{2}}^{x^{3}}\frac{dt}{\log t},x> 0\]
then
a) f' (x) = - 1/6 log x
b) f is an increasing function
c) f is an increasing function on \[\left(1 ,\infty\right)\]
d) Both b and c

View Answer

68. If \[I=\int_{0}^{1/2}\frac{d x}{\sqrt{1-x^{2n}}}\]
for n \[\geq1\] , the value of I is
a) less than 1
b) more than 1/2
c) more than 1
d) Both a and b

View Answer

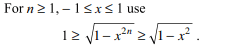
69.The value of \[\int_{3}^{4}\frac{d x}{\sqrt[3]{\log x}}\]
is
a) less than one
b) greater than 1/2
c) less than two
d) Both a and b

View Answer

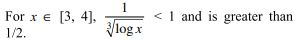
70. The absolute value of \[\int_{10}^{19}\frac{\sin x}{1+x^{8}}dx\]
is
a) less than \[10^{-7}\]
b) more than \[10^{-7}\]
c) less than \[10^{-6}\]
d) Both a and c

View Answer