1. A body is thrown vertically upwards with velocity u. The distance travelled by it in the fifth and the
sixth seconds are equal. The velocity u is given by\[\left(g=9.8 m\diagup s^{2}\right)\]
a) 24.5 m/s
b) 49.0 m/s
c) 73.5 m/s
d) 98.0 m/s
Explanation:
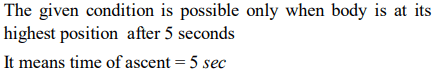
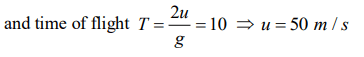
2. A body, thrown upwards with some velocity reaches the maximum height of 50 m. Another body with double the mass thrown up with double
the initial velocity will reach a maximum height of
a) 100 m
b) 200 m
c) 300 m
d) 400 m
Explanation:

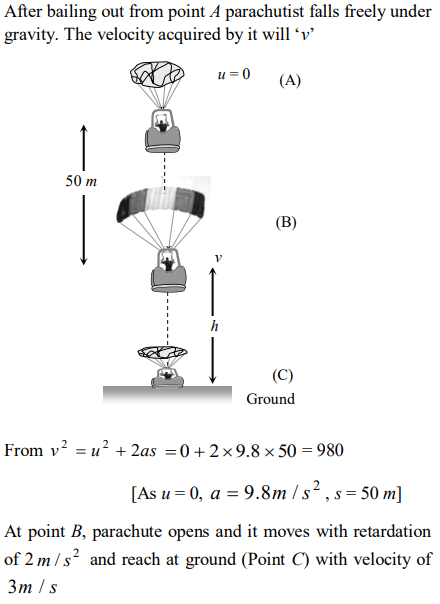
3. A parachutist after bailing out falls 50 m without friction. When parachute opens, it decelerates at \[2 m\diagup s^{2}\]. He reaches the ground with a speed of 3
m/s. At what height, did he bail out ?
a) 293 m
b) 111 m
c) 91 m
d) 182 m
Explanation:
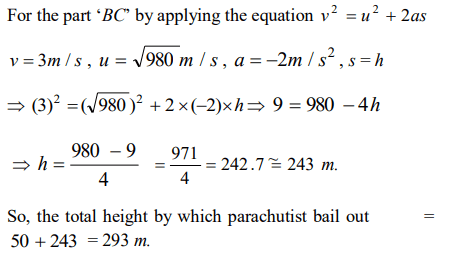
4. Three particles A, B and C are thrown from the top of a tower with the same speed. A is thrown up, B is thrown down and C is horizontally. They
hit the ground with speeds \[V_{A},V_{B}\] and \[V_{c}\] respectively
a) \[V_{A}=V_{B}= V_{c}\]
b) \[V_{A}=V_{B}>V_{c}\]
c) \[V_{A}>V_{B}>V_{c}\]
d) \[V_{A}>V_{B}=V_{c}\]
Explanation: \[V_{A}=V_{B}= V_{c}\]
5. From the top of a tower two stones, whose masses are in the ratio 1 : 2 are thrown one straight up with an initial speed u and the second straight
down with the same speed u. Then, neglecting air resistance
a) The heavier stone hits the ground with a higher speed
b) The lighter stone hits the ground with a higher speed
c) Both the stones will have the same speed when they hit the ground
d) The speed can't be determined with the given data.
Explanation: Both the stones will have the same speed when they hit the ground
6. An object start sliding on a frictionless inclined plane and from same height another object start falling freely
a) Both will reach with same speed
b) Both will reach with same acceleration
c) Both will reach in same time
d) None of above
Explanation: Both will reach with same speed
7. A particle moving in a straight line covers half the istance with speed of 3 m/s. The other half of the distance is covered in two equal time intervals
with speed of 4.5 m/s and 7.5 m/s respectively. The average speed of the particle during this motion is
a) 4.0 m/s
b) 5.0 m/s
c) 5.5 m/s
d) 4.8 m/s
Explanation:
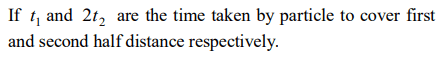
8. The acceleration of a particle is increasing linearly with time t as bt . The particle starts from the origin with an initial velocity \[V_{0}\] The
distance travelled by the particle in time t will be
a) \[V_{0}t+\frac{1}{3}bt^{2}\]
b) \[V_{0}t+\frac{1}{3}bt^{3}\]
c) \[V_{0}t+\frac{1}{6}bt^{3}\]
d) \[V_{0}t+\frac{1}{2}bt^{2}\]
Explanation:
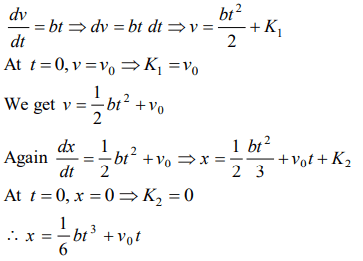
9. The motion of a body is given by the equation \[\frac{dv\left(t\right)}{dt}=6.0 -3v\left(t\right)\] . where \[v\left(t\right)\] is speed in m / s and t
in sec . If body was at rest at \[t=0\]
a) The terminal speed is \[2.0m\diagup s\]
b) The speed varies with the time as \[v\left(t\right)=2\left(1-e^{-3t}\right)m\diagup s\]
c) The magnitude of the initial acceleration is \[6.0m\diagup s^{2}\]
d) All of the above
Explanation:
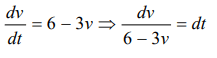
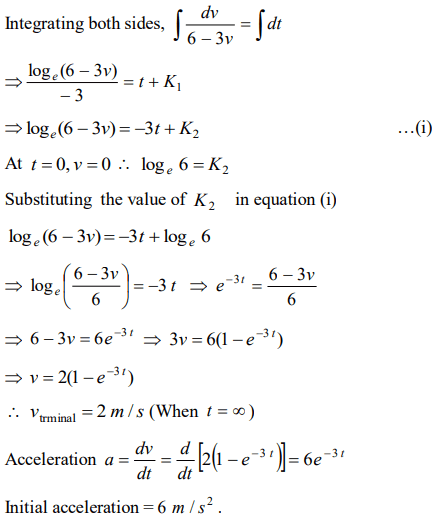
10. A particle of mass m moves on the x-axis as follows : it starts from rest at \[t=0\] from the point \[x=0\] and comes to rest at \[t=1\] at the point \[x=1\] . No other information is available about its motion
at intermediate time \[\left(0<t<1\right)\] . If \[\alpha\] denotes the instantaneous acceleration of the particle, then
a) \[\alpha\] cannot remain positive for all t in the interval \[0 \leq t\leq 1\]
b) \[\alpha\] must change sign during the motion but no other assertion can be made with the information given
c) |\[\alpha\]| must be \[\geq 4\] at some point or points in its path
d) Both a and b
Explanation: The body starts from rest at x = 0 and then again comes to rest at x = 1 . It means initially acceleration is positive and then negative.
So we can conclude that \[\alpha\] can not remains positive for all t in the interval 0 \[\leq\] t \[\leq\] 1 i.e. \[\alpha\] must change sign during the motion.