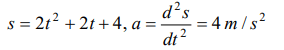1. A particle travels 10m in first 5 sec and 10m in next 3 sec. Assuming constant acceleration what is the distance travelled in next 2 sec
a) 8.3 m
b) 9.3 m
c) 10.3 m
d) None of above
Explanation:
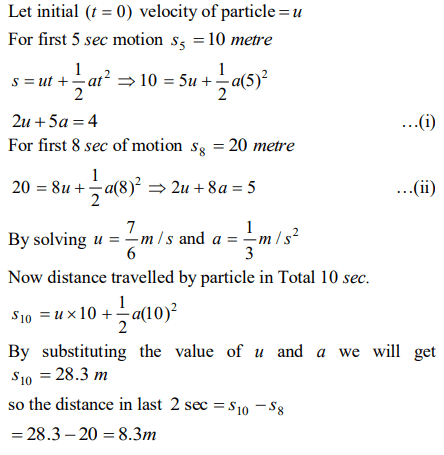
2. The distance travelled by a particle is proportional to the squares of time, then the particle travels with
a) Uniform acceleration
b) Uniform velocity
c) Increasing acceleration
d) Decreasing velocity
Explanation:
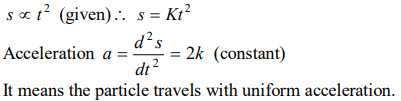
3. Acceleration of a particle changes when
a) Direction of velocity changes
b) Magnitude of velocity changes
c) Both of above
d) Speed changes
Explanation: Because acceleration is a vector quantity
4. The motion of a particle is described by the equation \[u=at\] . The distance travelled by the particle in the first 4 seconds
a) 4a
b) 12a
c) 6a
d) 8a
Explanation:
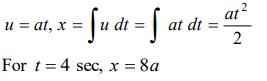
5. The relation \[3t=\sqrt{3x}+6\] describes the displacement of a particle in one direction where x is in metres and t in sec. The displacement,
when velocity is zero, is
a) 24 metres
b) 12 metres
c) 5 metres
d) Zero
Explanation:
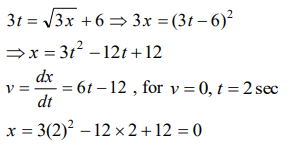
6. A constant force acts on a body of mass 0.9 kg at rest for 10s. If the body moves a distance of 250 m, the magnitude of the force is
a) 3N
b) 3.5N
c) 4.0N
d) 4.5N
Explanation:
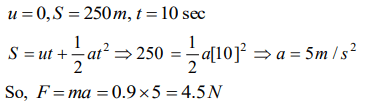
7. The average velocity of a body moving with uniform acceleration travelling a distance of 3.06 m is \[0.34 ms^{-1} \]. If the change in velocity of the body
is \[0.18 ms^{-1} \] during this time, its uniform acceleration is
a) \[0.01 ms^{-2} \]
b) \[0.02 ms^{-2} \]
c) \[0.03 ms^{-2} \]
d) \[0.04 ms^{-2} \]
Explanation:
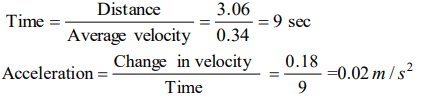
8. Equation of displacement for any particle is \[s=3t^{3} +7t^{2}+14t+8m\] . Its acceleration at time \[t=1\] sec is
a) \[10 m\diagup s^{2}\]
b) \[16 m\diagup s^{2}\]
c) \[25 m\diagup s^{2}\]
d) \[32 m\diagup s^{2}\]
Explanation:
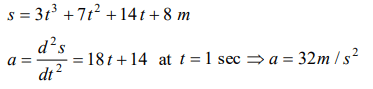
9. Consider the acceleration, velocity and displacement of a tennis ball as it falls to the ground and bounces back. Directions of which of these changes in the process
a) Velocity only
b) Displacement and velocity
c) Acceleration, velocity and displacement
d) Displacement and acceleration
Explanation: Only direction of displacement and velocity gets changed, acceleration is always directed vertically downward.
10. The displacement of a particle, moving in a straight line, is given by \[S=2t^{2} +2t+4\] where s is
in metres and t in seconds. The acceleration of
a) \[2 m\diagup s^{2}\]
b) \[4 m\diagup s^{2}\]
c) \[6 m\diagup s^{2}\]
d) \[8 m\diagup s^{2}\]
Explanation: