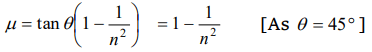1. A body of mass 5kg rests on a rough horizontal surface of coefficient of friction 0.2. The body is pulled through a distance of 10m by a horizontal force of 25 N. The kinetic
energy acquired by it is \[\left(g = 10 m/s^{2}\right)\]
a) 330 J
b) 150 J
c) 100 J
d) 50 J
Explanation:
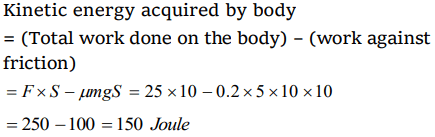
2. A motorcycle is travelling on a curved track of radius 500m. If the coefficient of friction between road and tyres is 0.5, the speed avoiding skidding will be
a) 50 m/s
b) 75 m/s
c) 25 m/s
d) 35 m/s
Explanation:
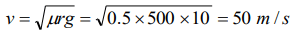
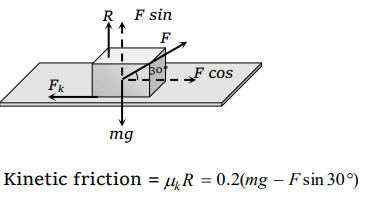
3. A block of mass \[m=5 kg\] is resting on a rough horizontal surface for which the coefficient of friction is 0.2. When a force \[F=40 N\] is applied, the acceleration of the block will be\[\left(g=10 m/s^{2}\right)\]
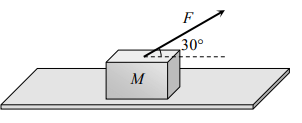
a) 5.73 \[m\diagup s^{2}\]
b) 8.0 \[m\diagup s^{2}\]
c) 3.17 \[m\diagup s^{2}\]
d) 10.0 \[m\diagup s^{2}\]
Explanation:
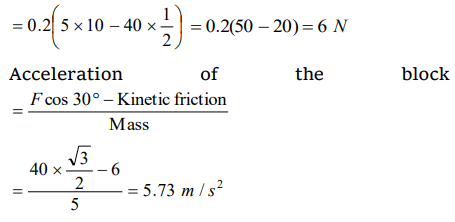
4. A body is moving along a rough horizontal surface with an
initial velocity 6 m/s. If the body comes to rest after
travelling 9 m, then the coefficient of sliding friction will be
a) 0.4
b) 0.2
c) 0.6
d) 0.8
Explanation:
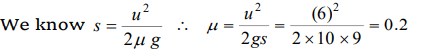
5. Consider a car moving on a straight road with a speed of 100 m/s. The distance at which car can be stopped is\[\left[\mu_{k}=0.5\right]\]
a) 100 m
b) 400 m
c) 800 m
d) 1000 m
Explanation:
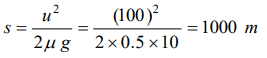
6. A cylinder of 10 kg is sliding in a plane with an initial velocity of 10 m/s. If the coefficient of friction between the surface and cylinder is 0.5 then before stopping, it will cover.
\[\left(g = 10 m\diagup s^{2}\right)\]
a) 2.5 m
b) 5 m
c) 7.5 m
d) 10 m
Explanation:
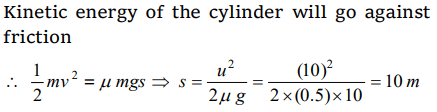
7. When a body is lying on a rough inclined plane and does not move, the force of friction
a) is equal to \[\mu R\]
b) is less than \[\mu R\]
c) is greater than\[\mu R\]
d) is equal to R
Explanation: When the body is at rest then static friction works on it, which is less than limiting friction (\[\mu\] R).
8. When a body is placed on a rough plane inclined at an angle \[\theta\] to the horizontal, its acceleration is
a) \[g\left(\sin\theta-\cos\theta\right)\]
b) \[g\left(\sin\theta-\mu\cos\theta\right)\]
c) \[g\left(\mu\sin\theta-\cos\theta\right)\]
d) \[g\mu\left(\sin\theta-\cos\theta\right)\]
Explanation: \[g\left(\sin\theta-\mu\cos\theta\right)\]
9. A block is at rest on an inclined plane making an angle \[\alpha\] with the horizontal. As the angle \[\alpha\] of the incline is increased, the block starts slipping when the angle of inclination becomes \[\theta\].
The coefficient of static friction between the block and the surface of the inclined plane is or A body starts sliding down at an angle \[\theta\] to horizontal. Then
coefficient of friction is equal to
a) \[\sin\theta\]
b) \[\cos\theta\]
c) \[\tan\theta\]
d) Independent of \[\theta\]
Explanation:
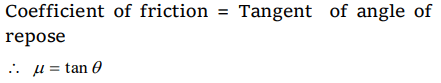
10.A given object takes n times as much time to slide down a 45° rough incline as it takes to slide down a perfectly smooth 45° incline. The coefficient of kinetic friction between the object
and the incline is given by
a) \[\left[1-\frac{1}{n^{2}}\right]\]
b) \[1-\frac{1}{n^{2}}\]
c) \[\sqrt{\left[1-\frac{1}{n^{2}}\right]}\]
d) \[\sqrt{n-\frac{1}{n^{2}}}\]
Explanation: