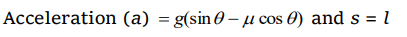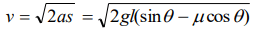1. A body is sliding down an inclined plane having coefficient of friction 0.5. If the normal reaction is twice that of the resultant downward force along the incline, the angle between the
inclined plane and the horizontal is
a) \[15^{\circ}\]
b) \[30^{\circ}\]
c) \[45^{\circ}\]
d) \[60^{\circ}\]
Explanation:
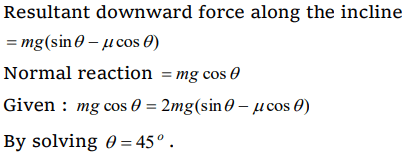
2. A body of mass 10 kg is lying on a rough plane inclined at an angle of \[30^{\circ}\] to the horizontal and the coefficient of friction is 0.5. the minimum force required to pull the body up the plane
is
a) 914 N
b) 91.4 N
c) 9.14 N
d) 0.914 N
Explanation:
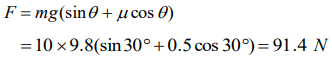
3. A block of mass 1 kg slides down on a rough inclined plane of inclination \[60^{\circ}\] starting from its top. If the coefficient of kinetic friction is 0.5 and length of the plane is 1 m, then work done
against friction is (Take g = 9.8 \[m\diagup s^{2}\] )
a) 9.82 J
b) 4.94 J
c) 2.45J
d) 1.96 J
Explanation:
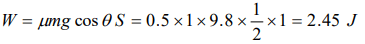
4. A block of mass 10 kg is placed on an inclined plane. When the angle of inclination is \[30^{\circ}\], the block just begins to slide down the plane. The force of static friction is
a) 10 kg wt
b) 89 kg wt
c) 49 kg wt
d) 5 kg wt
Explanation: F = mg sin 300 = 50 N = 5kg -wt
5. A body of 5 kg weight kept on a rough inclined plane of angle \[30^{\circ}\] starts sliding with a constant velocity. Then the coefficient of friction is (assume g = 10 \[m\diagup s^{2}\] )
a) \[1\diagup\sqrt{3}\]
b) \[2\diagup\sqrt{3}\]
c) \[\sqrt{3}\]
d) \[2\sqrt{3}\]
Explanation:
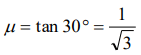
6. 300 Joule of work is done in sliding up a 2 kg block on an inclined plane to a height of 10 metres. Taking value of acceleration due to gravity ‘g’ to be \[10m\diagup s^{2}\], work done against
friction is
a) 100 J
b) 200 J
c) 300 J
d) Zero
Explanation: Work done against gravity = mgh = 2 * 10 * 10 = 200 J
Work done against friction = (Total work done – work done against gravity) = 300 - 200 = 100 J
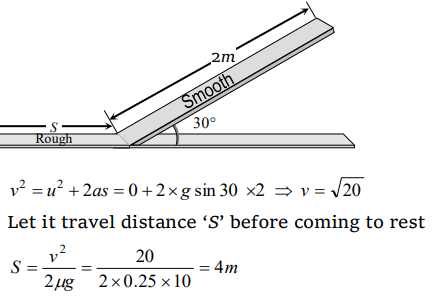
7. A 2 kg mass starts from rest on an inclined smooth surface with inclination \[30^{\circ}\] and length 2 m. How much will it travel beforecoming to rest on a frictional surface with frictional coefficient
of 0.25
a) 4 m
b) 6 m
c) 8 m
d) 2 m
Explanation:
8.A block rests on a rough inclined plane making an angle of \[30^{\circ}\] with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on
the block is 10 N, the mass of the block (in kg) is (Take g = 10 \[m\diagup s^{2}\] )
a) 2.0
b) 4.0
c) 1.6
d) 2.5
Explanation:
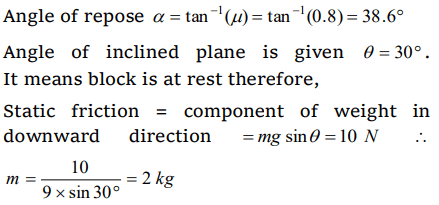
9. A body takes time t to reach the bottom of an inclined plane of angle \[\theta\] with the horizontal. If the plane is made rough, time taken now is 2t. The coefficient of friction of the rough surface
is
a) \[\frac{3}{4}\tan\theta\]
b) \[\frac{2}{3}\tan\theta\]
c) \[\frac{1}{4}\tan\theta\]
d) \[\frac{1}{2}\tan\theta\]
Explanation:
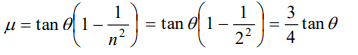
10.A block is kept on an inclined plane of inclination \[\theta\] of length l. The velocity of particle at the bottom of inclined is (the coefficient of friction is \[\mu\])
a) \[\sqrt{2gl\left(\mu\cos\theta-\sin\theta\right)}\]
b) \[\sqrt{2gl\left(\sin\theta-\mu\cos\theta\right)}\]
c) \[\sqrt{2gl\left(\sin\theta+\mu\cos\theta\right)}\]
d) \[\sqrt{2gl\left(\cos\theta+\mu\sin\theta\right)}\]
Explanation: