1. The force required just to move a body up an inclined plane is double the force required just to prevent the body sliding down.If the coefficient of friction is 0.25, the angle of inclination of
the plane is
a) 36.8°
b) 45°
c) 30°
d) 42.6°
Explanation:

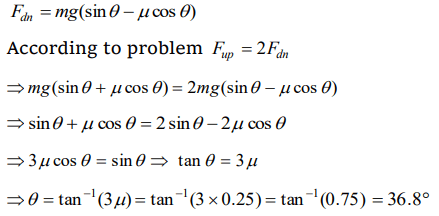
2. Starting from rest, a body slides down a 45° inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of friction between the body
and the inclined plane is
a) 0.33
b) 0.25
c) 0.75
d) 0.80
Explanation:
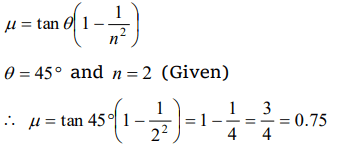
3.The coefficient of friction between a body and the surface of an inclined plane at 45° is 0.5. If \[g=9.8 m\diagup s^{2}\] , the acceleration of the body downwards in \[ m\diagup s^{2}\] is
a) \[\frac{4.9}{\sqrt{2}}\]
b) \[{4.9\sqrt{2}}\]
c) \[{19.6\sqrt{2}}\]
d) 4.9
Explanation:
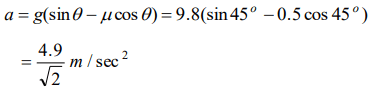
4. A box is placed on an inclined plane and has to be pushed down. The angle of inclination is
a) Equal to angle of friction
b) More than angle of friction
c) Equal to angle of repose
d) Less than angle of repose
Explanation: Because if the angle of inclination is equal to or more than angle of repose then box will automatically slides down the plane.
5. A force of 750 N is applied to a block of mass 102 kg to prevent it from sliding on a plane with an inclination angle 30° with the horizontal. If the coefficients of static friction and kinetic
friction between the block and the plane are 0.4 and 0.3 respectively, then the frictional force acting on the block is
a) 750 N
b) 500 N
c) 345 N
d) 250 N
Explanation:

6. A block is lying on an inclined plane which makes 60° with the horizontal. If coefficient of friction between block and plane is 0.25 and \[g=10 m\diagup s^{2}\] , then acceleration of the block when it
moves along the plane will be
a) 2.50 \[m\diagup s^{2}\]
b) 5.00 \[m\diagup s^{2}\]
c) 7.4 \[m\diagup s^{2}\]
d) 8.66 \[m\diagup s^{2}\]
Explanation:
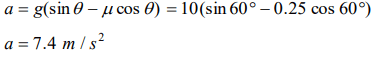
7. A body of mass 100 g is sliding from an inclined plane of inclination 30°. What is the frictional force experienced if \[\mu=1.7\]
a) \[1.7\times\sqrt{2}\times\frac{1}{\sqrt{3}}N\]
b) \[1.7\times\sqrt{3}\times\frac{1}{2}N\]
c) \[1.7\times\sqrt{3}N\]
d) \[1.7\times\sqrt{2}\times\frac{1}{3}N\]
Explanation:
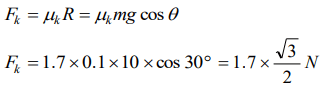
8.A body takes just twice the time as long to slide down a plane inclined at 30o to the horizontal as if the plane were frictionless. The coefficient of friction between the body and the plane is
a) \[\frac{\sqrt{3}}{4}\]
b) \[\sqrt{3}\]
c) \[\frac{4}{3}\]
d) \[\frac{3}{4}\]
Explanation:
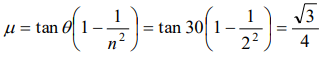
9.A brick of mass 2 kg begins to slide down on a plane inclined at an angle of \[45^{\circ}\] with the horizontal. The force of friction will
a) \[19.6\sin45^{\circ}\]
b) \[19.6\cos45^{\circ}\]
c) \[9.8\sin45^{\circ}\]
d) \[9.8\cos45^{\circ}\]
Explanation: For angle of repose, Friction = Component of weight along the plane
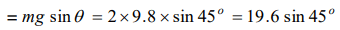
10. The upper half of an inclined plane of inclination \[\theta\] is perfectly smooth while the lower half is rough. A body starting from therest at top comes back to rest at the bottom if the coefficient of
friction for the lower half is given by
a) \[\mu =\sin\theta\]
b) \[\mu =\cot\theta\]
c) \[\mu =2\cos\theta\]
d) \[\mu =2\tan\theta\]
Explanation: For upper half
