1. The mass of the earth is \[6.00\times 10^{24}kg\] and that of the moon is \[7.40\times 10^{22}kg\] . The constant of gravitation \[G=6.67\times 10^{-11}N-m^{2}\diagup kg^{2}\] . The
potential energy of the system is \[-7.79\times 10^{28}\] joules. The mean distance between the earth and moon is
a) \[3.80\times 10^{8}metres\]
b) \[3.37\times 10^{6}metres\]
c) \[7.60\times 10^{4}metres\]
d) \[1.90\times 10^{2}metres\]
Explanation:
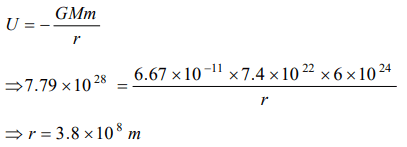
2. The change in potential energy, when a body of mass m is raised to a height nR from the earth's surface is (R = Radius of earth)
a) \[mgR \frac{n}{n-1}\]
b) nmgR
c) \[mgR \frac{n^{2}}{n^{2}+1}\]
d) \[mgR \frac{n}{n+1}\]
Explanation:
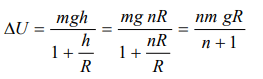
3. The masses and radii of the earth and moon are \[M_{1}, R_{1}\] and \[M_{2}, R_{2}\] respectively. Their centres are
distance d apart. The minimum velocity with which a particle of mass m should be projected from a point midway between their centres so
that it escapes to infinity is
a) \[2\sqrt{\frac{G}{d}\left(M_{1}+M_{2}\right)}\]
b) \[2\sqrt{\frac{2G}{d}\left(M_{1}+M_{2}\right)}\]
c) \[2\sqrt{\frac{Gm}{d}\left(M_{1}+M_{2}\right)}\]
d) \[2\sqrt{\frac{Gm\left(M_{1}+M_{2}\right)}{d\left(R_{1}+R_{2}\right)}}\]
Explanation:
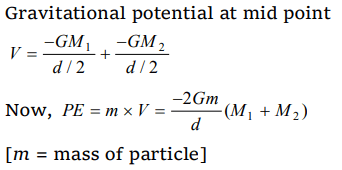
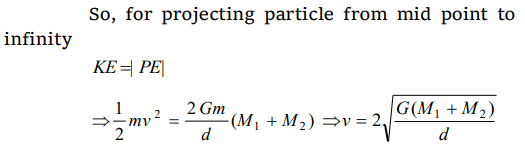
4. If mass of earth is M, radius is R and gravitational constant is G, then work done to take 1 kg mass from earth surface to infinity will be
a) \[\sqrt{\frac{Gm}{2R}}\]
b) \[\frac{GM}{R}\]
c) \[\sqrt{\frac{2Gm}{R}}\]
d) \[\frac{Gm}{2R}\]
Explanation: Potential energy of the 1 kg mass which is placed at the earth surface = \[\frac{-GM}{R}\]
its potential energy at infinite = 0
Work done = change in potential energy = \[\frac{GM}{R}\]
5.A rocket is launched with velocity 10 km/s. If radius of earth is R, then maximum height attained by it will be
a) 2R
b) 3R
c) 4R
d) 5R
Explanation: 4R
6. There are two bodies of masses 100 kg and 10000 kg separated by a distance 1 m. At what distance from the smaller body, the intensity of
gravitational field will be zero
a)\[\frac{1}{9}m\]
b) \[\frac{1}{10}m\]
c) \[\frac{1}{11}m\]
d) \[\frac{10}{11}m\]
Explanation:
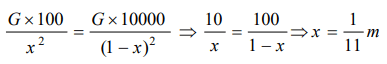
7. What is the intensity of gravitational field of the centre of a spherical shell
a) \[Gm\diagup r^{2}\]
b) g
c) Zero
d) none of these
Explanation: Zero
8. The gravitational potential energy of a body of mass ‘m’ at the earth’s surface \[-mgR_{e}\] . Its gravitational potential energy at a height Re from the earth’s surface will be (Here Re is the radius of the earth)
a) \[-2mgR_{e}\]
b) \[2mgR_{e}\]
c) \[\frac{1}{2}mgR_{e}\]
d) \[-\frac{1}{2}mgR_{e}\]
Explanation:
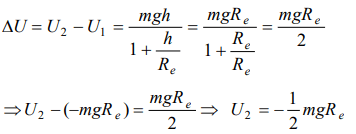
9. Escape velocity of a body of 1 kg mass on a planet is 100 m/sec. Gravitational Potential energy of the body at the Planet is
a) – 5000 J
b) – 1000 J
c) – 2400 J
d) 5000 J
Explanation:
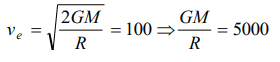
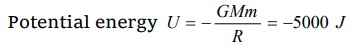
10. A body of mass m is placed on the earth’s surface. It is taken from the earth’s surface to a height \[h=3R\] . The change in gravitational potential energy of the body is
a) \[\frac{2}{3}mgR\]
b) \[\frac{3}{4}mgR\]
c) \[\frac{mgR}{2}\]
d) \[\frac{mgR}{4}\]
Explanation:
