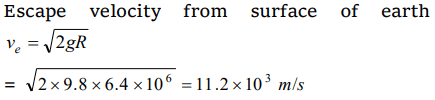1. The escape velocity from the surface of earth is \[ V_{e}\] . The escape velocity from the surface of a planet whose mass and radius are 3 times those of
the earth will be
a) \[ V_{e}\]
b) \[ 3 V_{e}\]
c) \[9 V_{e}\]
d) \[ 27 V_{e}\]
Explanation:
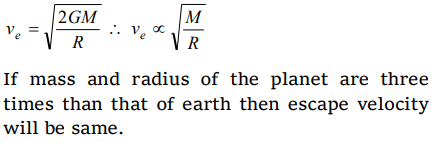
2.How much energy will be necessary for making a body of 500 kg escape from the earth [g = 9.8 m/s2, radius of earth = 6.4 * 106 m]
a) About \[9.8\times 10^{6}J\]
b) About \[6.4\times 10^{8}J\]
c) About \[3.1\times 10^{10}J\]
d) About \[27.4\times 10^{12}J\]
Explanation:
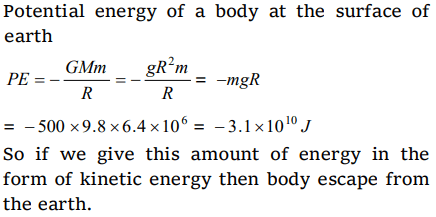
3. The escape velocity for the earth is 11.2 km/sec. The mass of another planet is 100 times that of the earth and its radius is 4 times that of the
earth. The escape velocity for this planet will be
a) 112.0 km/s
b) 5.6 km/s
c) 280.0 km/s
d) 56.0 km/s
Explanation:
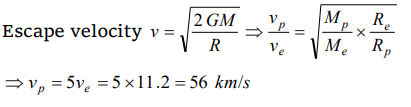
4. The escape velocity of a planet having mass 6 times and radius 2 times as that of earth is
a) \[ \sqrt{3} V_{e}\]
b) \[ 3 V_{e}\]
c) \[ \sqrt{2} V_{e}\]
d) \[ 2 V_{e}\]
Explanation:
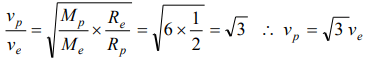
5. The escape velocity of an object on a planet whose g value is 9 times on earth and whose radius is 4 times that of earth in km/s is
a) 67.2
b) 33.6
c) 16.8
d) 25.2
Explanation:
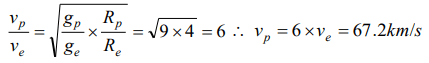
6. The escape velocity on earth is 11.2 km/s. On another planet having twice radius and 8 times mass of the earth, the escape velocity will be
a) 3.7 km/s
b) 11.2 km/s
c) 22.4 km/s
d) 42.4 km/s
Explanation:
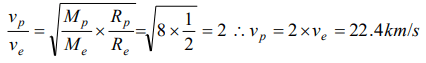
7.The escape velocity of a body on the surface of the earth is 11.2 km/s. If the earth's mass increases to twice its present value and the radius of the earth becomes half, the escape velocity
would become
a) 5.6 km/s
b) 11.2 km/s (remain unchanged)
c) 22.4 km/s
d) 44.8 km/s
Explanation:
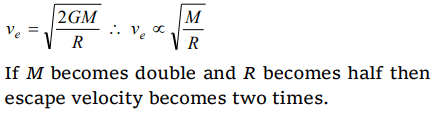
8. Given mass of the moon is 1/81 of the mass of the earth and corresponding radius is 1/4 of the earth. If escape velocity on the earth surface is 11.2 km/s, the value of same on the surface of the
moon is
a) 0.14 km/s
b) 0.5 km/s
c) 2.5 km/s
d) 5 km/s
Explanation:
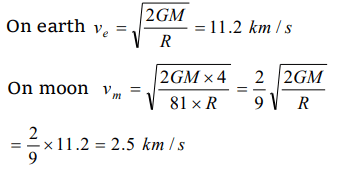
9. The angular velocity of rotation of star (of mass M and radius R) at which the matter start to escape from its equator will be
a) \[\sqrt{\frac{2GM^{2}}{R}}\]
b) \[\sqrt{\frac{2GM}{g}}\]
c) \[\sqrt{\frac{2GM}{R^{3}}}\]
d) \[\sqrt{\frac{2GR}{M}}\]
Explanation:
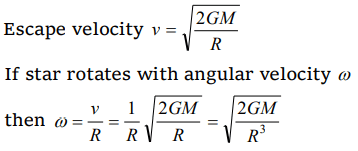
10. The least velocity required to throw a body away from the surface of a planet so that it may not return is (radius of the planet is \[6.4\times10^{6} m,g=9.8 m/sec^{2}\] )
a) \[9.8\times10^{-3} m/sec\]
b) \[12.8\times10^{3} m/sec\]
c) \[9.8\times10^{3} m/sec\]
d) \[11.2\times10^{3} m/sec\]
Explanation: