1.A body weighs 700 gm wt on the surface of the earth. How much will it weigh on the surface of a
planet whose mass is \[\frac{1}{7}\] and radius is half that of the earth
a) 200 gm wt
b) 400 gm wt
c) 50 gm wt
d) 300 gm wt
Explanation:
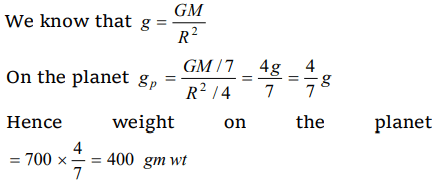
2. In order to find time, the astronaut orbiting in an earth satellite should use
a) A pendulum clock
b) A watch having main spring to keep it going
c) Either a pendulum clock or a watch
d) Neither a pendulum clock nor a watch
Explanation: In pendulum clock the time period depends on the value of g, while in spring watch, the time period is independent of the value of g
3. A spherical planet far out in space has a mass \[M_{0}\] and diameter \[D_{0}\] . A particle of mass m falling
freely near the surface of this planet will experience an acceleration due to gravity which is equal to
a) \[GM_{0}\diagup D_0^2\]
b) \[4mGM_{0}\diagup D_0^2\]
c) \[4GM_{0}\diagup D_0^2\]
d) \[GmM_{0}\diagup D_0^2\]
Explanation:
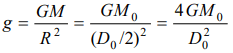
4.If the earth stops rotating, the value of ‘g’ at the equator will
a) Increase
b) Remain same
c) Decrease
d) None of the above
Explanation: Increase
5. The mass and diameter of a planet have twice the value of the corresponding parameters of earth.Acceleration due to gravity on the surface of the
planet is
a) 9.8 \[m\diagup sec^{2}\]
b) 4.9 \[m\diagup sec^{2}\]
c) 980 \[m\diagup sec^{2}\]
d) 19.6 \[m\diagup sec^{2}\]
Explanation:

6. As we go from the equator to the poles, the value of g
a) Remains the same
b) Decreases
c) Increases
d) Decreases upto a latitude of 45°
Explanation: Increases
7. Force of gravity is least at
a) The equator
b) The poles
c) A point in between equator and any pole
d) none of these
Explanation: The equator
8. The radius of the earth is 6400 km and \[g=10 m\diagup sec^{2}\] . In order that a body of 5 kg weighs zero at the equator, the angular speed of the earth
is
a) 1/80 radian/sec
b) 1/400 radian/sec
c) 1/800 radian/sec
d) 1/1600 radian/sec
Explanation:

9. The value of ‘g’ at a particular point is \[9.8 m\diagup sec^{2}\] . Suppose the earth suddenly shrinks uniformly to
half its present size without losing any mass. The value of ‘g’ at the same point (assuming that the distance of the point from the centre of earth does
not shrink) will now be
a) 4.9 \[m\diagup sec^{2}\]
b) 3.1 \[m\diagup sec^{2}\]
c) 9.8 \[m\diagup sec^{2}\]
d) 19.6 \[m\diagup sec^{2}\]
Explanation:
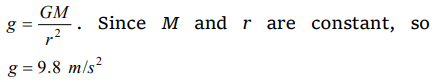
10. If R is the radius of the earth and g the acceleration due to gravity on the earth's surface, the mean density of the earth is
a) \[4\pi G\diagup 3gR\]
b) \[3\pi R\diagup 4gG\]
c) \[3 g\diagup 4 \pi RG\]
d) \[\pi RG\diagup 12G\]
Explanation:
