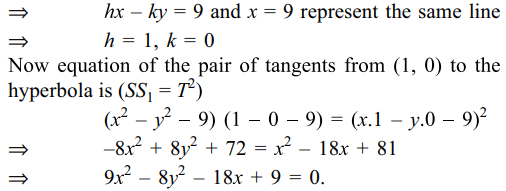1. The equation of the hyperbola whose conjugate axis is 5 and distance between the foci is 13, is
a) \[25x^{2}-144y^{2}=900\]
b) \[144x^{2}-25y^{2}=900\]
c) \[25x^{2}-36y^{2}=900\]
d) \[36x^{2}-25y^{2}=900\]
Explanation:
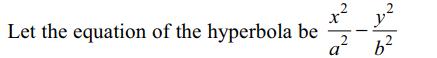
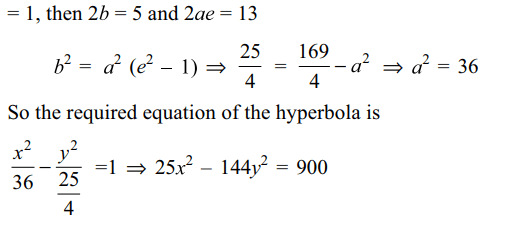
2. The vertices of a hyperbola are (0,0) and (10,0). If one of its foci is (18,0) , the equation
of the hyperbola is
a) \[\frac{x^{2}}{25}-\frac{y^{2}}{144}=1\]
b) \[\frac{\left(x-5\right)^{2}}{25}-\frac{y^{2}}{144}=1\]
c) \[\frac{x^{2}}{25}-\frac{\left(y-5\right)^{2}}{144}=1\]
d) \[\frac{\left(x-5\right)^{2}}{25}-\frac{\left(y-5\right)^{2}}{144}=1\]
Explanation: Centre of the hyperbola is the mid point (5,0)
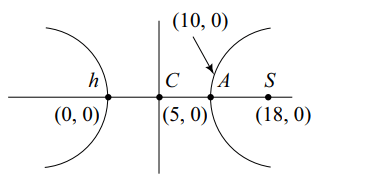
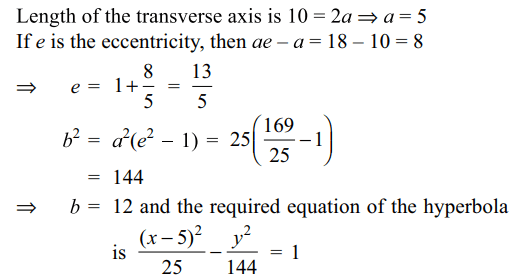
3.The equation of the hyperbola whose foci
are (6,4) and (-4,4) and eccentricity 2 is given by
a) \[12x^{2}-4y^{2}+24x-32y-127=0\]
b) \[12x^{2}-4y^{2}-24x+32y-127=0\]
c) \[12x^{2}-4y^{2}+24x+32y+127=0\]
d) \[12x^{2}-4y^{2}-24x+32y+127=0\]
Explanation: Center is the midpoint (1,4) of the foci
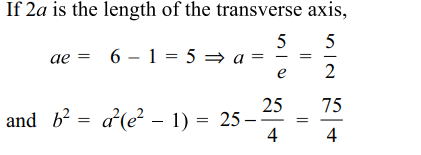
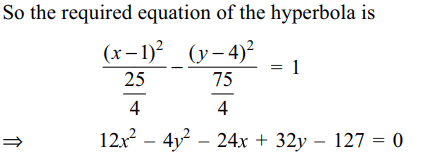
4. If \[m_{1},m_{2}\] are the slopes of the tangents to
the hyperbola \[\frac{x^{2}}{144}-\frac{y^{2}}{25}=1\] which pass through the point
(14,6) , then
a) \[m_{1}+m_{2}=\frac{42}{13}\]
b) \[m_{1}m_{2}=\frac{11}{52}\]
c) \[m_{1}+m_{2}=\frac{51}{52}\]
d) \[m_{1}m_{2}=\frac{42}{13}\]
Explanation: Equation of a line through (14,6) is
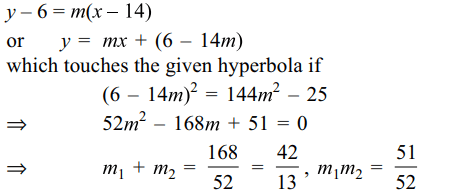
5. The value of m, for which the line \[y=mx+\frac{25\sqrt{3}}{3}\] is a normal to the hyperbola \[\frac{x^{2}}{16}-\frac{y^{2}}{9}=1\]
is
a) \[\sqrt{3}\]
b) \[-\frac{2}{\sqrt{3}}\]
c) \[-\frac{\sqrt{3}}{2}\]
d) 1
Explanation: Equation of a normal to the given hyperbola is
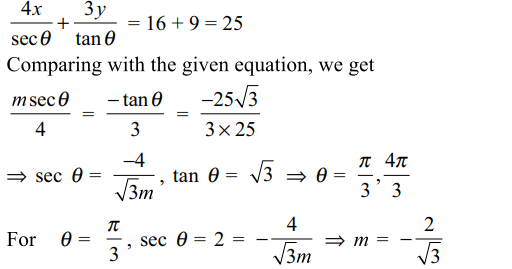
6. Let \[P\left(a\sec \theta,b\tan\theta\right)\] and \[Q\left(a\sec \phi,b\tan\phi\right)\] where
\[\theta+\phi=\pi/2,\] be two points on the hyperbola
\[x^{2}/a^{2}-y^{2}/b^{2}=1.\] If (h, k) is the point of intersection of
normals at P and Q, then k is equal to
a) \[\frac{a^{2}+b^{2}}{a}\]
b) \[-\left[\frac{a^{2}+b^{2}}{a}\right]\]
c) \[\frac{a^{2}+b^{2}}{b}\]
d) \[-\left[\frac{a^{2}+b^{2}}{b}\right]\]
Explanation: Equation of the normal at P is
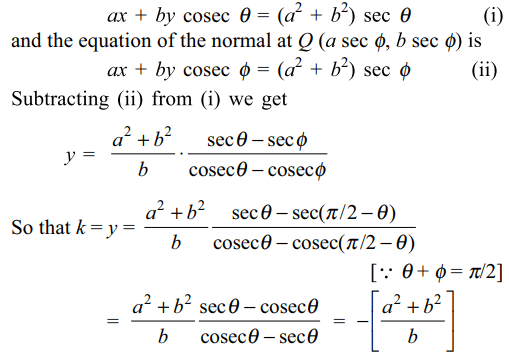
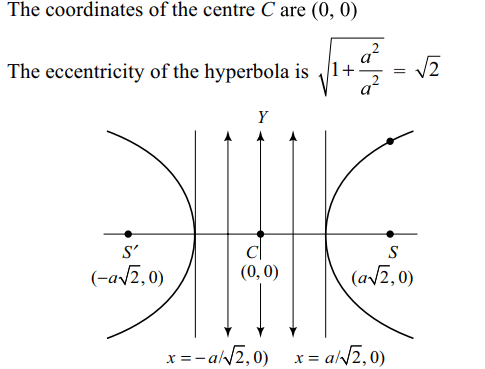
7. If P is a point on the rectangular hyperbola
\[x^{2}-y^{2}=a^{2},C\] is its centre and S, S' are the two foci, then
SP. S'P =
a) 2
b) \[\left(CP\right)^{2}\]
c) \[\left(CS\right)^{2}\]
d) \[\left(SS'\right)^{2}\]
Explanation: Let the coordinates of P be (x, y)

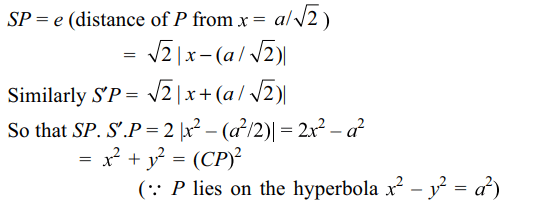
8. If PQ is a double ordinate of the hyperbola \[\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\] such that OPQ is an equilateral triangle, O
being the centre of the hyperbola. Then the eccentricity e of the hyperbola, satisfies
a) \[1< e< 2/\sqrt{3}\]
b) \[e=2/\sqrt{3}\]
c) \[e=\sqrt{3}/2\]
d) \[e>2/\sqrt{3}\]
Explanation: Let the coordinates of P be ( \[\alpha,\beta\] )
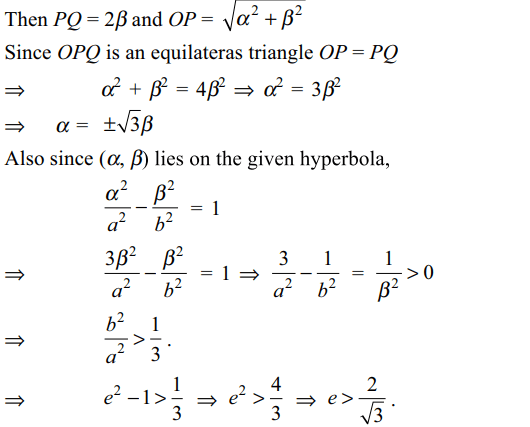
9. Let a and b be non-zero real numbers.
Then the equation \[\left(ax^{2}+by^{2}+c\right)\left(x^{2}-5xy+6y^{2}\right)=0\]
represents
a) Four straight lines ,when c =0 and a,b are
of the same sign.
b) Two straight lines and a circle ,when a=b and c and a are of the same sign.
c) Two straight lines and a hyperbola ,when a and b are of opposite sign
d) a circle and an ellipse , when a and b are of the same sign and c is of sign opposite to that of a.
Explanation:
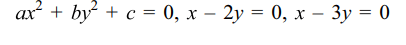
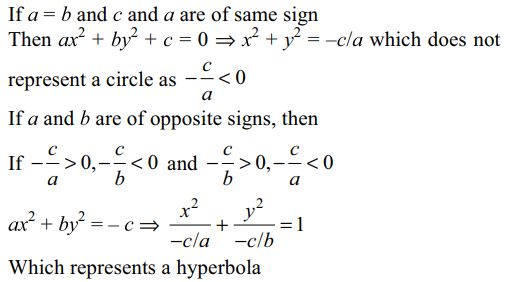
10. If x= 9 is the chord of contact of the
hyperbola \[x^{2}-y^{2}=9\] , then the equation of the corresponding
pair of tangents is
a) \[9x^{2}-8y^{2}+18x-9=0\]
b) \[9x^{2}-8y^{2}-18x+9=0\]
c) \[9x^{2}-8y^{2}-18x-9=0\]
d) \[9x^{2}-8y^{2}+18x+9=0\]
Explanation: Let (h, k) be the point whose chord of contact w.r.t the hyperbola x2 – y2 = 9 is x = 9