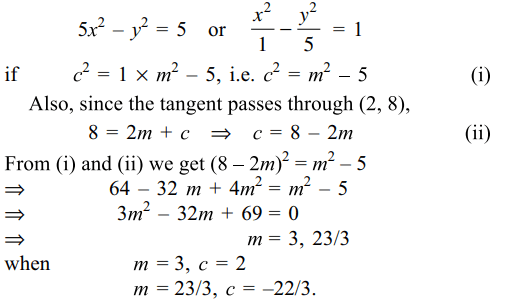1. If the angle between a pair of tangents
from a point P to the parabola \[y^{2}=4ax\] is \[\frac{\pi}{4}\] then the locus
of P is a hyperbola whose equation is
a) \[x^{2}-y^{2}=8a^{2}\]
b) \[\left(x-3a\right)^{2}-y^{2}=8a^{2}\]
c) \[\left(x+3a\right)^{2}-y^{2}=8a^{2}\]
d) \[x^{2}-y^{2}=a^{2}\]
Explanation: Let P( \[\alpha,\beta\] ) be any point on the locus. Equation of pair of tangents from P( \[\alpha,\beta\] ) to the parabola y2 = 4ax is
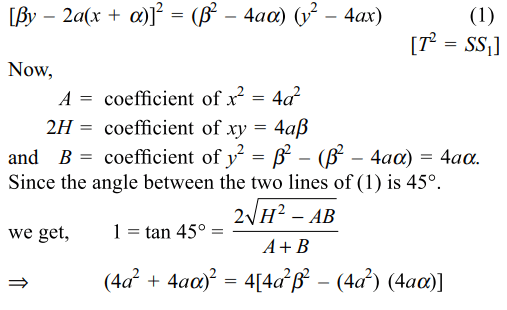
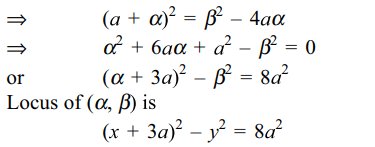
2. Tangents are drawn to the circle \[x^{2}+y^{2}=9\] from points on the hyperbola \[\frac{x^{2}}{9}-\frac{y^{2}}{4}=1.\] Locus of the
mid point of the chords of contact is
a) a circle
b) an ellipse
c) a hyperbola
d) none of these
Explanation:
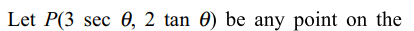


3. If \[0<\alpha<\pi/2,\alpha\neq\frac{\pi}{4}\] then for the
hyperbola \[\frac{x^{2}}{\left(\cos\alpha+\sin\alpha\right)^{2}}-\frac{y^{2}}{\left(\cos\alpha-\sin\alpha\right)^{2}}=1\]
which one of the following is independent of \[\alpha\]
a) eccentricity
b) directrix
c) abscissa of vertices
d) acissa of foci
Explanation:
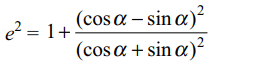

4. All chords of the curve \[3x^{2}-y^{2}-2x+4y=0\] which subtend a right at the origin pass through
a) centre of the rectangular hyperbola \[x^{2}-y^{2}-2x-4y=12\]
b) the point of intersection of the lines y+2x=0 and x=1
c) the vertex of the parabola \[x^{2}-2x-4y-7=0\]
d) All of the Above
Explanation: Let y = mx + c be a chord of the given curve.


5. The equation of a tangent to the hyperbola
\[3x^{2}-y^{2}=3\] , parallel to the line y = 2x + 4 is
a) y = 2x + 3
b) y = 2x + 1
c) y = 2x - 1
d) Both b and c
Explanation: The equation of the hyperbola is

6. If a variable straight line x cos \[\alpha+y\sin \alpha=p\] which is a chord of the hyperbola \[\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\] ( b > 0)
subtend a right angle at the centre of the hyperbola , then it always touches a fixed circle whose
a) centre is the centre of the hyperbola
b) radius is \[\frac{ab}{\sqrt{b^{2}-a^{2}}}\]
c) centre (0,0)
d) All of the Above
Explanation: Equation of the pair of straight lines passing

7. An ellipse intersects the hyperbola
\[2x^{2}-2y^{2}=1\] orthogonally. The eccentricity of the ellipse is
reciprocal of that of the hyperbola. If the axes of the ellipse are along
the coordinates axes, then
a) Equation of ellipse is \[x^{2}+2y^{2}=2\]
b) The foci of ellipse are \[\left(\pm1,0\right)\]
c) Equation of ellipse is \[x^{2}+2y^{2}=4\]
d) Both a and b
Explanation:

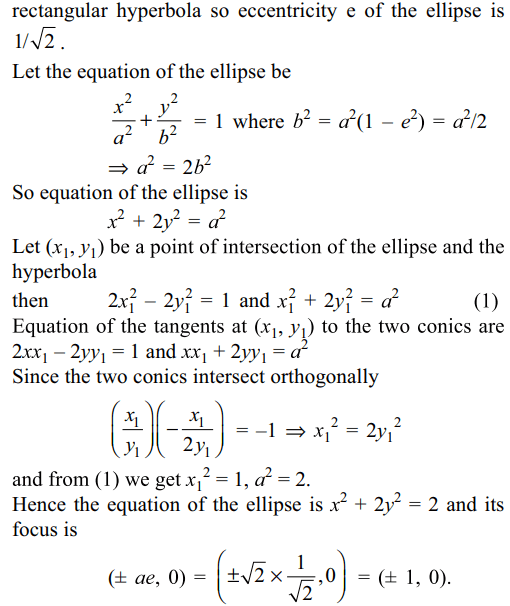
8. If the circle \[x^{2}+y^{2}=a^{2}\] intersect the
hyperbola \[xy=c^{2}\] in four points \[P\left(x_{1},y_{1}\right),Q\left(x_{2},y_{2}\right),R\left(x_{3},y_{3}\right),S\left(x_{4},y_{4}\right)\]
then
a) \[x_{1}+x_{2}+x_{3}+x_{4}=0\]
b) \[x_{1}x_{2}x_{3}x_{4}=e^{4}\]
c) \[y_{1}+y_{2}+y_{3}+y_{4}=0\]
d) All of the Above
Explanation: The abscissa of the points of intersection of
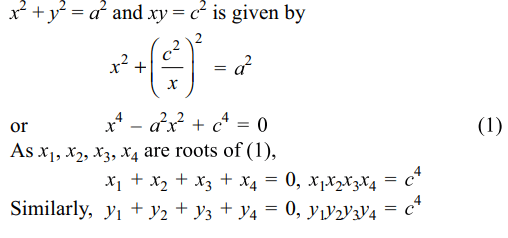
9. If the normals at four points \[\left(x_{1},y_{1}\right),\left(x_{2},y_{2}\right),\left(x_{3},y_{3}\right), and \left(x_{4},y_{4}\right)\]
on the rectangular hyperbola xy = c2 meets at point (h, k) , then
a) \[x_{1}+x_{2}+x_{3}+x_{4}=h\]
b) \[y_{1}+y_{2}+y_{3}+y_{4}=k\]
c) \[x_{1}x_{2}x_{3}x_{4}=-c^{4}\]
d) All of the Above
Explanation:

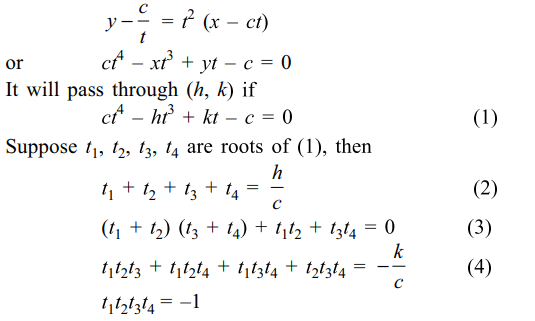
10. Equation of a tangent passing throught (2,8) to the hyperbola \[5x^{2}-y^{2}=5\]
a) \[3x-y+2=0\]
b) \[3x+y+14=0\]
c) \[23x-3y-22=0\]
d) Both a and c
Explanation: y = mx + c is a tangent to the hyperbola,