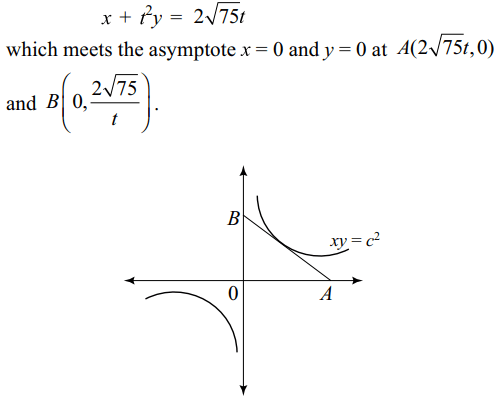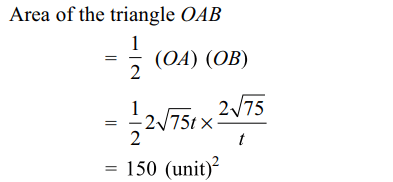1. Consider a branch of the hyperbola \[x^{2}-2y^{2}-2\sqrt{2}x-4\sqrt{2}y-6=0\]
with vertex at the point A.
Let B be one of the end points of its latus rectum. If C is
the focus of the hyperbola nearest to the point A, the area
of the triangle ABC is
a) \[1-\sqrt{2/3}\]
b) \[\sqrt{3/2}-1\]
c) \[1+\sqrt{2/3}\]
d) \[\sqrt{3/2}+1\]
Explanation: Equation of the branch of the hyperbola can be written as
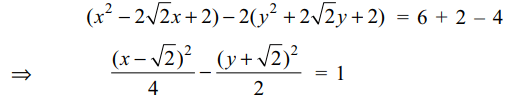
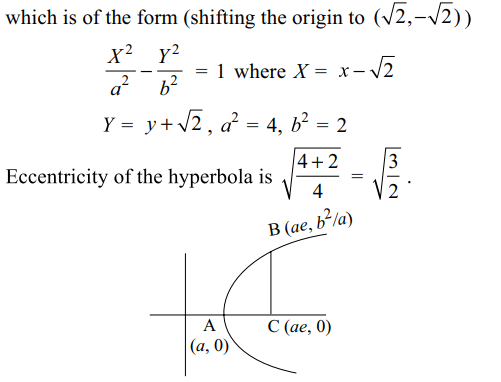

2. The tangent at any point P( a sec \[\theta\] , b tan \[\theta\] )
of the hyperbola \[x^{2}/a^{2}-y^{2}/b^{2}=1\] makes an intercept of
length p between the point of contact and the transvers axis
of the hyperbola. p1, p2 are the lengths of the perpendiculars
drawn from the foci on the normal at P, then
a) p is an arithmetic mean between \[P_{1}\] and \[P_{2}\]
b) p is a geometric mean between \[P_{1}\] and \[P_{2}\]
c) p is a harmonic mean between \[P_{1}\] and \[P_{2}\]
d) none of these
Explanation:
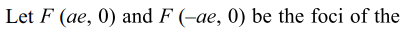
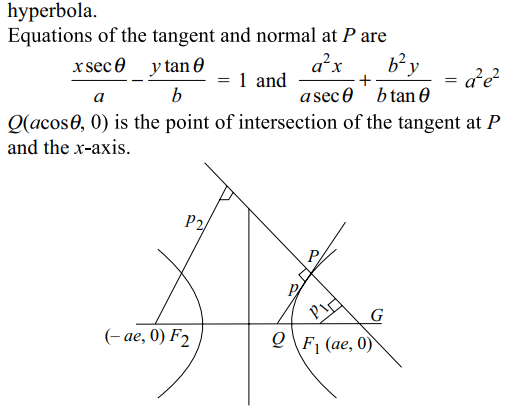

3. Let a> 0 and A(-a,0) and (a,0) be two fixed points. Let a point
P moves such that base angles
of the triangle PAB be such then \[\angle PAB=2\angle PBA \] , then P
traces
a) a straight lines
b) a circle
c) an ellipse
d) a hyperbola
Explanation: Suppose coordinates of P be (h, k) Slope of
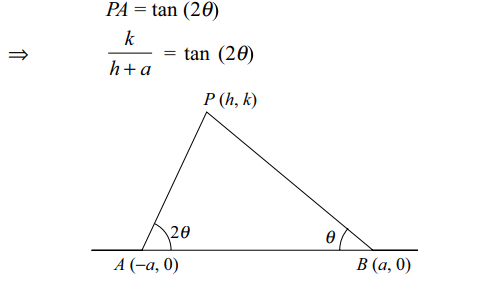

4. Suppose base BC of a triangle is of
fixed lenth "a" and its vertex A moves such that the ratio \[\frac{\tan\left(B/2\right)}{\tan\left(C/2\right)}\] is a constant \[k\neq 1\] , then A traces
a) a circle
b) an ellipse
c) a hyperbola
d) a parabola
Explanation:
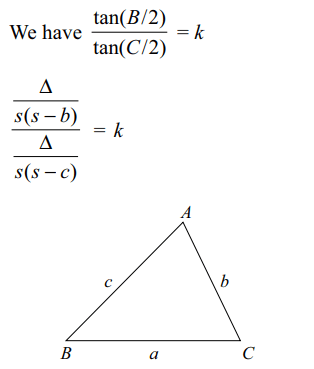

5. \[x=a\cos\theta+b\sin\theta,y=a\sin\theta-b\cos\theta , a,b>0\]
represents a rectangular hyperbola if
a) \[0<\theta<\frac{\pi}{4}\]
b) \[\frac{\pi}{4}<\theta<\frac{3\pi}{4}\]
c) \[0\leq\theta\leq\frac{\pi}{2}\]
d) \[\frac{3\pi}{2}<\theta<\pi\]
Explanation:

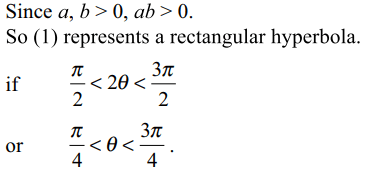
6. Tangent at a point P to the rectangular
hyperbola xy= 20 where it intersects the rectangular
hyperbola \[x^{2}-y^{2}=9\] is
a) \[4x+5y\pm40=0\]
b) \[4x\pm5y+40=0\]
c) \[4x\pm5y-40=0\]
d) \[4x+5y\pm20=0\]
Explanation: For the coordinates of P,
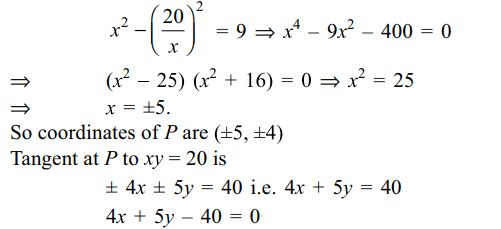
7. If x+ y =b is a tangent to the hyperbola
xy= 9, then b equals
a) \[\pm 3\]
b) \[\pm 6\]
c) \[\pm 1\]
d) \[\pm 9\]
Explanation: An equation of the tangent at (3t, 3/t) to the curve xy = 9 is
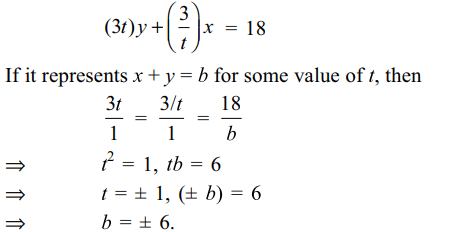
8. If x = 9 is the chord of contact of the
hyperbola \[x^{2}-y^{2}=9\] , then the equation of the corresponding
pair of tangents are
a) \[2\sqrt{2x}\pm3y+8=0\]
b) \[3x\pm2\sqrt{2y}-3=0\]
c) \[2x\pm2\sqrt{2y}+7=0\]
d) \[x\pm2\sqrt{2y}+8=0\]
Explanation: Let (h, k) be the point such that the chord of contact of (h, k) with respect to the hyperbola x2 – y2 = 9 is x = 9. We know that chord of contact of (h, k) with respect to x2 – y2 = 9 is T = 0, i.e., hx – ky – 9 = 0
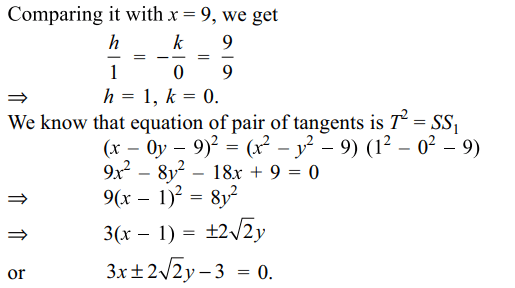
9. Let \[A_{i}\left(t_{i},\frac{c}{t_{i}}\right)i=1,2,3\] be three points
on the rectangular hyperbola \[xy=c^{2}\] , then the orthocenter of
the triangle \[A_{1}A_{2}A_{3}\] lies on
a) x-axis
b) y-axis
c) \[xy=c^{2}\]
d) \[x^{2}-y^{2}=c^{2}\]
Explanation:


10. Area of the triangle formed by a tangent
to the hyperbola xy= 75 and its asymptotes is
a) \[25\left(unit\right)^{2}\]
b) \[50\left(unit\right)^{2}\]
c) \[100\left(unit\right)^{2}\]
d) \[150\left(unit\right)^{2}\]
Explanation:

hyperbola is