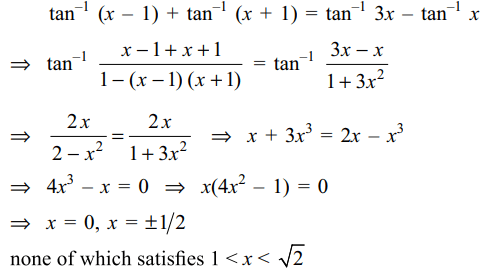1. The value of \[\cot \left[\sum_{n=1}^{23}\cot^{-1}\left(1+\sum_{k=1}^{n}2k\right)\right]\]
is
a) \[\frac{23}{25}\]
b) \[\frac{25}{23}\]
c) \[\frac{23}{24}\]
d) \[\frac{24}{23}\]
Explanation:
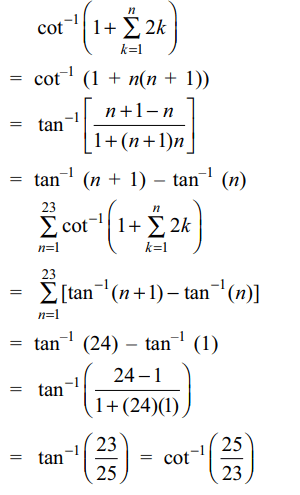
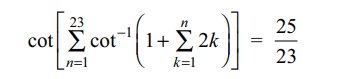
2. If \[\sin^{-1}\sqrt{x^{2}+2x+1}+\sec^{-1}\sqrt{x^{2}+2x+1}=\pi/2,x\neq 0\]
then the value of
\[2\sec^{-1}\left(\frac{x}{2}\right)+\sin^{-1}\left(\frac{x}{2}\right)\] is equal to
a) \[-\frac{3\pi}{2}\]
b) \[\frac{3\pi}{2}\]
c) \[-\frac{\pi}{2}\]
d) \[\frac{\pi}{2}\]
Explanation:
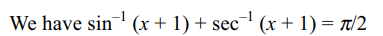
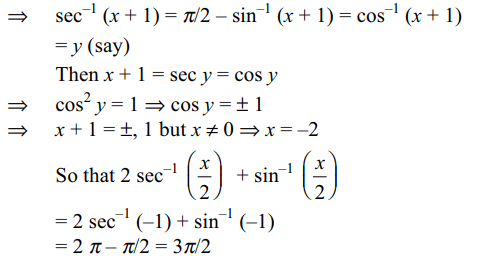
3. If 0 < x < 1, then\[\sqrt{1+x^{2}}\left[\left\{x\cos\left(\cot^{-1}x\right)+\sin\left(\cot^{-1}x\right)\right\}^{2}-1\right]^{1/2}\]
is equal to
a) \[\frac{x}{\sqrt{1+x^{2}}}\]
b) x
c) \[x\sqrt{1+x^{2}}\]
d) \[\sqrt{1+x^{2}}\]
Explanation:
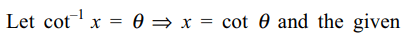
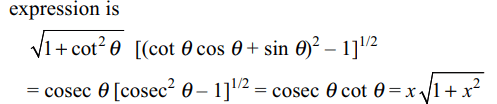
4. If \[\left(\tan^{-1}x\right)^{2}+\left(\cot^{-1}x\right)^{2}=5\pi^{2}/8\]
then x equal
a) 0
b) -1
c) -2
d) -3
Explanation:
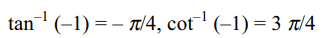
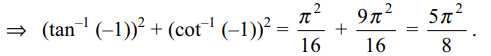
5. The number of solutions of the equation \[\sin^{-1}\left(\frac{1+x^{2}}{2 x}\right)=\frac{\pi}{2}\left(\sec\left(x-1\right)\right)\]
is/are
a) 0
b) 1
c) 2
d) 3
Explanation:

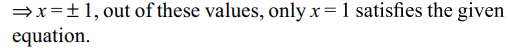
6. The number of positive integral solutions
of \[\tan^{-1}x+\cot^{-1}y=\tan^{-1}3\] is
a) 1
b) 2
c) 3
d) 4
Explanation:
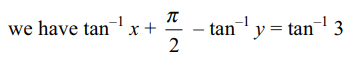
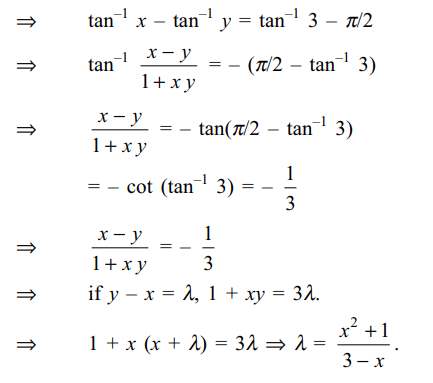
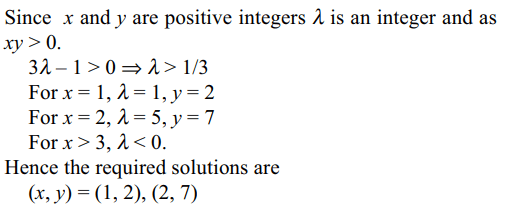
7. In a triangle ABC, if \[\cot A=\left(x^{3}+x^{2}+x\right)^{1/2} \cot B=\left(x+x^{-1}+1\right)^{1/2} and \cot C=\left(x^{-3}+x^{-2}+x^{-1}\right)^{-1/2}\]
then the triangle is
a) equilateral
b) isosceles
c) right angled
d) obtuse angled
Explanation: cot (A + B)
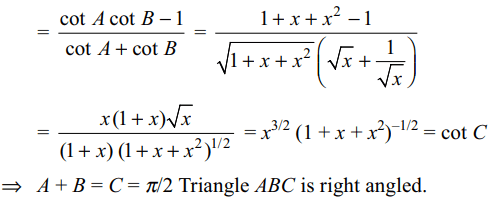
8. The value of \[\cos\left(\frac{1}{2}\cos^{-1}\frac{1}{8}\right)\] is equal to
a) 3/4
b) -3/4
c) 1/16
d) 1/4
Explanation:
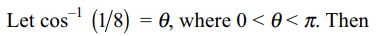
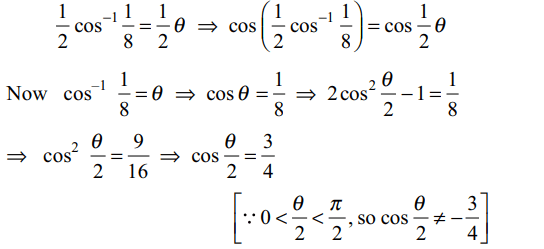
9. The inequality \[\sin^{-1}\left(\sin 5\right)> x^{2}-4x\] holds if
a) \[x=2-\sqrt{9-2\pi}\]
b) \[x=2+\sqrt{9-2\pi}\]
c) \[x\epsilon\left(2-\sqrt{9-2\pi},2+\sqrt{9-2\pi}\right)\]
d) \[x > 2+\sqrt{9-2\pi}\]
Explanation:
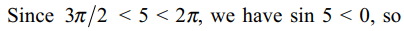
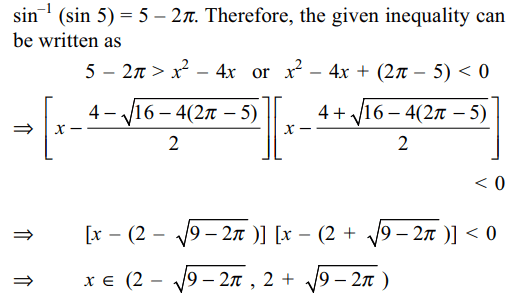
10. If \[1< x<\sqrt{2}\] , the number of solutions
of the equation
\[\tan^{-1}\left(x-1\right)+\tan^{-1}x+\tan^{-1}\left(x+1\right)=\tan^{-1}3x\]
is
a) 0
b) 1
c) 2
d) 3
Explanation: The given equation can be written as