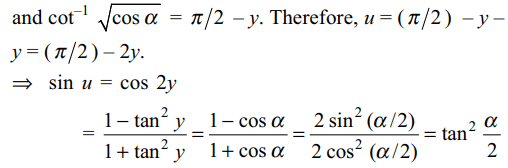1. If \[a\sin^{-1}x-b\cos^{-1}x=c\] , then \[a\sin^{-1}x+b\cos^{-1}x\] is equal to
a) 0
b) \[\frac{\pi ab+c\left(b-a\right)}{a+b}\]
c) \[\pi/2\]
d) \[\frac{\pi ab+c\left(a-b\right)}{a+b}\]
Explanation:

2. If \[\frac{1}{2}\sin^{-1}\left[\frac{3\sin2\theta}{5+4\cos 2\theta}\right]=\tan^{-1}x\]
then x =
a) \[\tan3\theta\]
b) \[3\tan\theta\]
c) \[\left(1/3\right)\tan\theta\]
d) \[3 \cot\theta\]
Explanation:


3. If x > 0, y > 0 and x > y, then \[\tan^{-1}\left(x/y\right)+\tan^{-1}[\left(x+y\right)/\left(x-y\right)]\]
is equal to
a) \[-\pi/4\]
b) \[\pi/4\]
c) \[3\pi/4\]
d) none of these
Explanation:
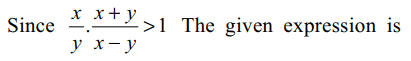

4. The equation \[2 \cos^{-1}x=\sin^{-1}\left(2x\sqrt{1-x^{2}}\right)\] is valid for all values of x satisfying
a) \[-1\leq x\leq 1\]
b) \[0\leq x\leq 1\]
c) \[-0\leq x\leq 1/\sqrt{2}\]
d) \[1/\sqrt{2}\leq x\leq 1\]
Explanation: If we denote cos- 1x by y, then
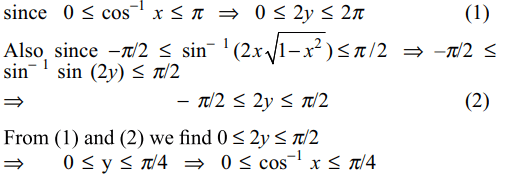

5. If \[\tan^{-1}\frac{1}{1+2}+\tan^{-1}\frac{1}{1+\left(2\right)\left(3\right)}+\tan^{-1}\frac{1}{1+\left(3\right)\left(4\right)}+....+\tan^{-1}\frac{1}{1+n\left(n+1\right)}=\tan^{-1}\theta\]
then \[\theta=\]
a) \[\frac{n}{n+1}\]
b) \[\frac{n+1}{n+2}\]
c) \[\frac{n}{n+2}\]
d) \[\frac{n-1}{n+2}\]
Explanation:
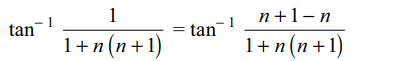
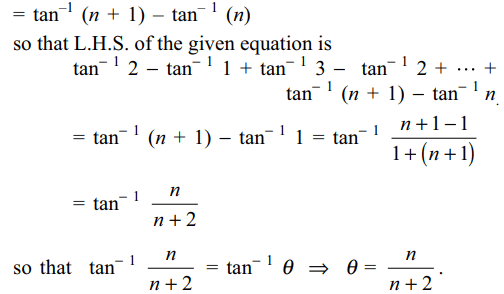
6. A root of the equation \[17x^{2}+17x \tan\left[2\tan^{-1}\left(1/5\right)-\pi/4\right]-10=0\]
is
a) 10/17
b) -1
c) -7/17
d) 1
Explanation:
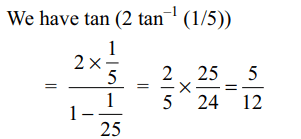
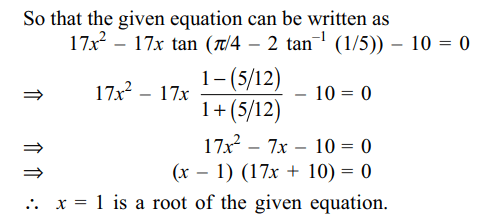
7. The value of \[\sin\left(2\tan^{-1}\left(1/3\right)\right)+\cos\left(\tan^{-1}2\sqrt{2}\right)\]
is
a) 12/13
b) 13/14
c) 14/15
d) none of these
Explanation:


8. The sum of the infinite series \[\cot^{-1}2+\cot^{-1}8+\cot^{-1}18+\cot^{-1}32+....\]
is equal to
a) \[\pi/3\]
b) \[\pi/4\]
c) \[\pi/6\]
d) \[\pi/8\]
Explanation: The nth term of the series can be written as

9. The value of \[\sin^{-1}\left\{\cot\left(\sin^{-1}\sqrt{\frac{2-\sqrt{3}}{4}}+\cos^{-1}\frac{\sqrt{12}}{4}+\sec^{-1}\sqrt{2}\right)\right\}\]
is equal to
a) \[\pi/4\]
b) \[\pi/6\]
c) 0
d) \[\pi/2\]
Explanation:
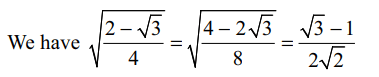


10. If \[u=\cot^{-1}\sqrt{\cos\alpha}-\tan^{-1}\sqrt{\cos\alpha},\]
then
sin u is equal to
a) \[\tan^{2}\left(\alpha/2\right)\]
b) \[\cot^{2}\left(\alpha/2\right)\]
c) \[\tan^{2}\alpha\]
d) \[\cot^{2}\alpha\]
Explanation: