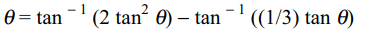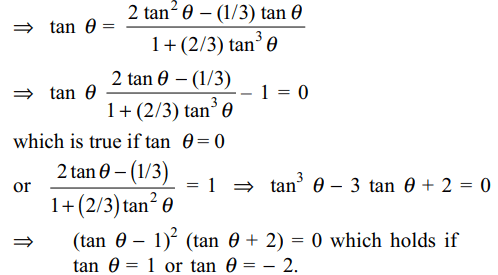1. The value of \[\cos^{-1}x+\cos^{-1}\left(\frac{x}{2}+\frac{1}{2}\sqrt{3-3x^{2}}\right)\left(1/2\leq x\leq1\right)\]
is equal to
a) \[\pi/6\]
b) \[\pi/3\]
c) \[\pi\]
d) 0
Explanation: Let cos–1 x = y. Then x = cos y, so that
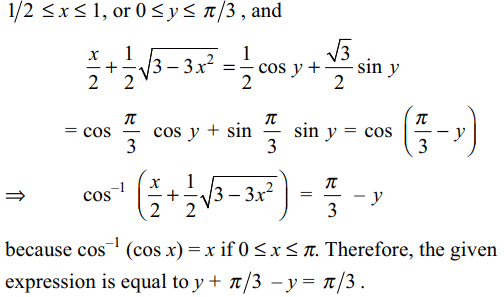
2. \[\sin^{-1}\left(\sin\left(\frac{2x^{2}+4}{1+x^{2}}\right)\right)<\pi-3\] if
a) \[-1\leq x \leq 0\]
b) \[0\leq x \leq 1\]
c) –1 < x < 1
d) x > 1
Explanation:
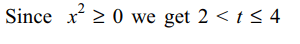
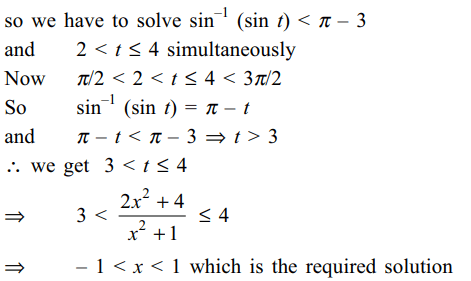
3. If \[\tan^{-1}\frac{\sqrt{1+x^{2}}-\sqrt{1-x^{2}}}{\sqrt{1+x^{2}}+\sqrt{1-x^{2}}}=\alpha\]
then \[x^{2} \] is equal to
a) \[\sin\alpha\]
b) \[\cos2\alpha\]
c) \[\cos\alpha\]
d) \[\sin2\alpha\]
Explanation: From the given relation we have

4. If \[\tan^{-1}\frac{a}{x}+\tan^{-1}\frac{b}{x}+\tan^{-1}\frac{c}{x}+\tan^{-1}\frac{d}{x}=\frac{\pi}{2}\]
then \[x^{4}-x^{2}\sum ab+abcd\] is equal to
a) -1
b) 0
c) 1
d) 2
Explanation:

5. If \[x_{1},x_{2},x_{3},x_{4}\] are roots of the equation
\[x^{4}-x^{3}\sin 2\beta+x^{2}\cos2\beta-x\cos\beta-\sin\beta=0\]
then
\[\sum_{i=1}^{4}\tan^{-1}x_{i}\] is equal to
a) \[\pi-\beta\]
b) \[\pi-2\beta\]
c) \[\left(\pi/2\right)-\beta\]
d) \[\left(\pi/2\right)-2\beta\]
Explanation:

6. If \[\alpha=3\sin^{-1}\left(\frac{6}{11}\right)\] and \[\beta=3\cos^{-1}\left(\frac{4}{9}\right)\] where the inverse trigonometric functions take only the
principal values, then the correct option (s) is (are)
a) \[\cos\alpha < 0\]
b) \[\sin\beta < 0\]
c) \[\cos\left(\alpha+\beta\right) > 0\]
d) All of the above
Explanation:
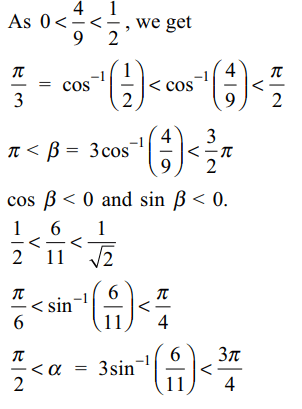

7. If the numerical value of \[\tan \left(\cos^{-1}\left(4/5\right)+\tan^{-1}\left(2/3\right)\right)\] is a/b then
a) a + b = 23
b) a – b = 11
c) 3b = a + 1
d) All of the Above
Explanation:
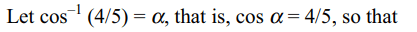
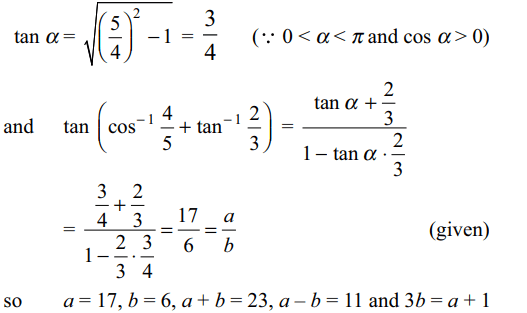
8. If \[a=\sin^{-1}\left(-\frac{\sqrt{2}}{2}\right)+\cos^{-1}\left(-\frac{1}{2}\right)\]
and \[b=\tan^{-1}\left(-\sqrt{3}\right)-\cot^{-1}\left(-\frac{1}{\sqrt{3}}\right)\]
then
a) \[a – b = 17\pi/12\]
b) \[a + b = 17\pi/12\]
c) \[a + b = -7\pi/12\]
d) Both a and c
Explanation:
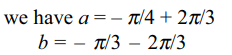
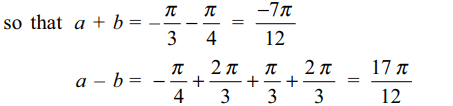
9. If \[\alpha,\beta\] are the roots of the equation \[\left(\tan^{-1}\left(x/5\right)\right)^{2}+\left(\sqrt{3}-1\right)\tan^{-1}\left(x/5\right)-\sqrt{3}=0 , \mid \alpha\mid >\mid\beta\mid\]
then
a) \[\alpha+\beta =-5\pi/12\]
b) \[\mid\alpha-\beta \mid=35\pi/12\]
c) \[\alpha\beta = -25\pi^{2}/12\]
d) All of the Above
Explanation:

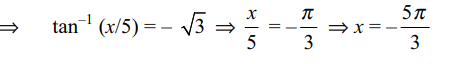

10. \[\theta=\tan^{-1}\left(2\tan^{2}\theta\right)-\tan^{-1}\left(\left(1/3\right)\tan\theta\right)\]
if
tan \[\theta\] is equal to
a) -2
b) 1
c) 2/3
d) Both a and b
Explanation: