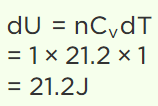1. A cylinder rolls without slipping down an inclined plane, the number of degrees of freedom it has, is
a) 2
b) 3
c) 5
d) 1
Explanation: A cylinder rolls without slipping down an inclined plane, the number of degrees of freedom it has, is 2
2. If the degree of freedom of a gas are f, then the ratio of two specific heats \[C_{P}\diagup C_{V}\] is given by
a) \[\frac{2}{f}+1\]
b) \[1-\frac{2}{f}\]
c) \[1+\frac{1}{f}\]
d) \[1-\frac{1}{f}\]
Explanation:
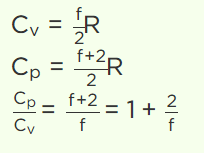
3. The degrees of freedom of a triatomic gas is
a) 2
b) 4
c) 6
d) 8
Explanation: The degrees of freedom of a triatomic gas is 6
4. A diatomic gas molecule has translational, rotational and vibrational degrees of freedom. The \[C_{P}\diagup C_{V}\] is
a) 1.67
b) 1.4
c) 1.29
d) 1.33
Explanation: A diatomic gas molecule has translational, rotational and vibrational degrees of freedom. The \[C_{P}\diagup C_{V}\] is 1.33
5. For a gas \[\frac{R}{C_{V}}=0.67\] . This gas is made up of molecules which are
a) Diatomic
b) Mixture of diatomic and polyatomic molecules
c) Monoatomic
d) Polyatomic
Explanation: For a gas \[\frac{R}{C_{V}}=0.67\] . This gas is made up of molecules which are Monoatomic
6. The value of CV for one mole of neon gas is
a) \[\frac{1}{2}R\]
b) \[\frac{3}{2}R\]
c) \[\frac{5}{2}R\]
d) \[\frac{7}{2}R\]
Explanation: The value of CV for one mole of neon gas is \[\frac{3}{2}R\]
7. For an ideal gas of diatomic molecules
a) \[C_{P}=\frac{5}{2}R\]
b) \[C_{V}=\frac{3}{2}R\]
c) \[C_{P}-C_{V}=2R\]
d) \[C_{P}=\frac{7}{2}R\]
Explanation: For an ideal gas of diatomic molecules, \[C_{P}=\frac{7}{2}R\]
8. At constant volume, for different diatomic gases the molar specific heat is
a) Same and 3 cal/mole/°C approximately
b) Exactly equal and its value is 4 cal/mole/°C
c) Will be totally different
d) Approximately equal and its value is 5
cal/mole/°C
Explanation: At constant volume, for different diatomic gases the molar specific heat is approximately equal and its value is 5 cal/mole/°C
9. At constant volume the specific heat of a gas is \[\frac{3R}{2}\] , then the value of '\[\gamma\] ' will be
a) \[\frac{3}{2}\]
b) \[\frac{5}{2}\]
c) \[\frac{5}{3}\]
d) None of the above
Explanation: \[\frac{5}{3}\]
10. The specific heat of a gas at constant volume is 21.2 J/mole/°C. If the temperature is increased by
1°C keeping the volume constant, the change in its internal energy will be
a) 0
b) 21.2 J
c) 42.2 J
d) 10.6 J
Explanation: