1. One mole of monoatomic gas and three moles of diatomic gas are put together in a container. The molar specific heat \[\left( J K^{-1}mol ^{-1}\right)\] at constant
volume is \[\left(R=8.3 J K^{-1}mol ^{-1}\right)\]
a) 18.7
b) 18.9
c) 19.2
d) None of the above
Explanation:
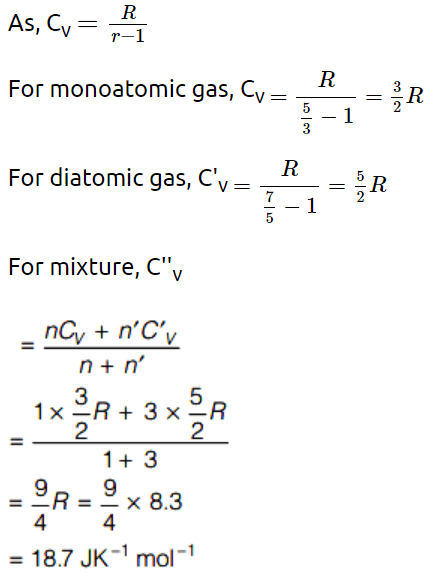
2. The temperature of argon, kept in a vessel, is raised by \[1 ^{\circ}C\] at a constant volume. The total heat supplied to the gas is a combination of
translational and rotational energies. Their respective shares are
a) 60% and 40%
b) 40% and 60%
c) 50% and 50%
d) 100% and 0%
Explanation: 100% and 0%
3. On giving equal amount of heat at constant volume to 1 mol of a monoatomic and a diatomic gas the rise in temperature \[\left(\triangle T\right)\] is more for
a) Monoatomic
b) Diatomic
c) Same for both
d) Can not be predicted
Explanation: Monoatomic
4. The kinetic energy, due to translational motion, of
most of the molecules of an ideal gas at absolute
temperature T is
a) kT
b) k/T
c) T/k
d) 1/kT
Explanation: kT
5. The number of translational degrees of freedom for a diatomic gas is
a) 2
b) 3
c) 5
d) 6
Explanation: The number of translational degrees of freedom for a diatomic gas is 3
6. The value of the gas constant (R) calculated from the perfect gas equation is 8.32 joules/gm mole K, whereas its value calculated from the knowledge
of \[C_{P}\] and \[C_{v}\] of the gas is 1.98 cal/gm mole K. From this data, the value of J is
a) 4.16 J / cal
b) 4.18 J / cal
c) 4.20 J / cal
d) 4.22 J / cal
Explanation: 4.20 J / cal
7. For a gas if ratio of specific heats at constant pressure and volume is \[\gamma\] then value of degrees of
freedom is
a) \[\frac{3\gamma-1}{2\gamma-1}\]
b) \[\frac{2}{\gamma-1}\]
c) \[\frac{9}{2}{\gamma-1}\]
d)\[\frac{25}{2}{\gamma-1}\]
Explanation: For a gas if ratio of specific heats at constant pressure and volume is \[\gamma\] then value of degrees of freedom is \[\frac{2}{\gamma-1}\]
8. The ratio of specific heat of a mixture of one mole of helium and one mole of hydrogen gas will be
a) 1
b) 1.5
c) 1.53
d) 1.33
Explanation: The ratio of specific heat of a mixture of one mole of helium and one mole of hydrogen gas will be 1.5
9. For a gas \[\gamma=7\diagup5\] . The gas may probably be
a) Helium
b) Hydrogen
c) Argon
d) Neon
Explanation: For a gas \[\gamma=7\diagup5\] . The gas may probably be Hydrogen
10. If a gas has n degrees of freedom ratio of specific heats of gas is
a) \[\frac{1+n}{2}\]
b) \[1+\frac{1}{n}\]
c) \[1+\frac{n}{2}\]
d) \[1+\frac{2}{n}\]
Explanation: If a gas has n degrees of freedom ratio of specific heats of gas is \[1+\frac{2}{n}\]