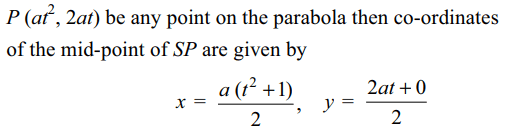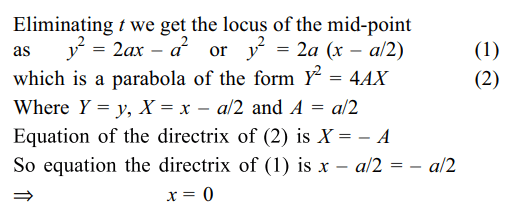1. Length of the chord of the parabola
\[y^{2}=4ax\] passing throught the vertex and making an angle
\[\theta\left(0<\theta<\pi\right)\] with the axis of the parabola is
a) \[4a\mid\cot\theta\mid cosec\theta\]
b) \[2a\mid\cot\theta\mid cosec\theta\]
c) \[a\mid\cot\theta\mid cosec\theta\]
d) \[a \cot^{3} q\]
Explanation:
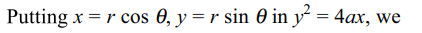
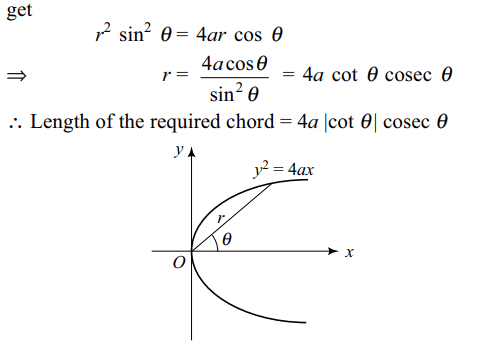
2. If \[r_{1} \] and \[r_{2} \] are length of two perpendicular chords of the parabola drawn thought the vertex , then value of \[16a^{2} \left[\left(r_{1}r_2^2\right)^{-\frac{2}{3}}+\left(r_1^2r_{2}\right)^{-\frac{2}{3}}\right]\]
is
a) \[\frac{1}{4}\]
b) \[\frac{1}{2}\]
c) 1
d) 2
Explanation:
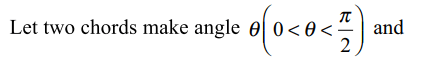
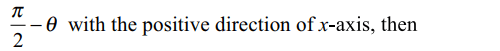
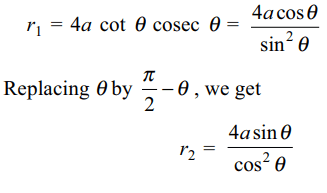
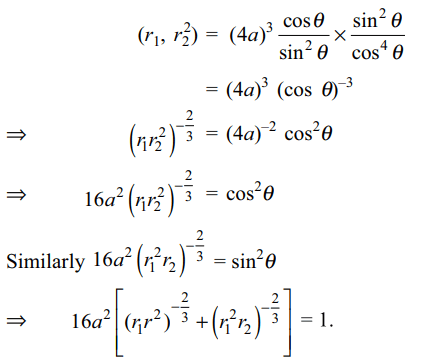
3. A point P moves such that the difference
between its distance from the origin and from the axis of x is always a constant c.
the locus of P is a
a) straight line having equal intercepts c on the axes
b) circle having its centre at (0, –c/2) and passing
through \[\left(c\sqrt{2},-c/2\right)\]
c) parabola with its vertex at (0, –c/2) and passing
through \[\left(c\sqrt{2},c/2\right)\]
d) none of these .
Explanation: Let the coordinates of P be (h, k)
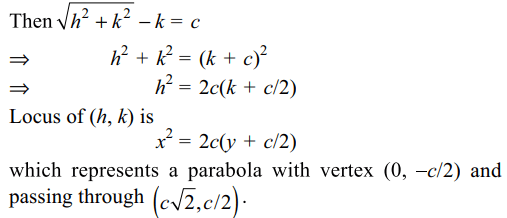
4. Shortest distance of the point (0, c) from
the parabola \[y=x^{2}\] where \[0\leq c\leq 5\]
is
a) c if \[0\leq c\leq 1/2\]
b) c if \[3\leq c\leq 5\]
c) \[\sqrt{c-1/4}\] if \[1/2\leq c\leq5\] , c if \[0\leq c \leq1/2\]
d) \[\sqrt{c}\]
Explanation: If S is the distance of the point (x, y) on the
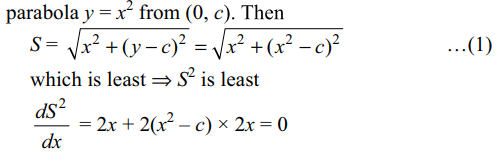
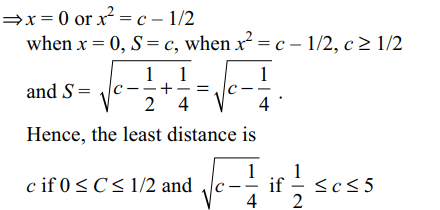
5. \[L_{1}\] and \[L_{2}\] are the length of the segments
of any focal chord of the parabola \[y^{2}=x\] , then \[\frac{1}{L_{1}}+\frac{1}{L_{2}}\] is
equal to
a) 2
b) 3
c) 4
d) none of these
Explanation: Any point on the parabola is P(at2 , 2at)
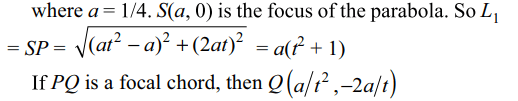
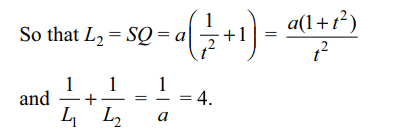
6. The length of the intercept on the normal at the point
\[\left(at^{2},2at\right)\] of the parabola \[y^{2}=4ax\] made by the
circle which is described on the focal distance of the given
point as diameter is
a) \[a\left(1+t^{2}\right)\]
b) \[a\sqrt{1+t^{2}}\]
c) \[\sqrt{a\left(1+t^{2}\right)}\]
d) none of these
Explanation:
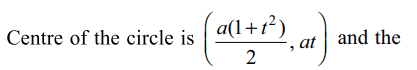

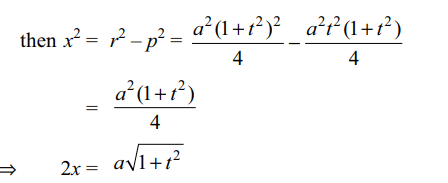
7. A line bisecting the ordinate PN of a point
P\[\left(at^{2},2at\right)\] , t > 0, on the parabola \[y^{2}=4ax\] is drawn parallel
to the axis to meet the curve at Q. If NQ meets the tangent
at the vertex at the point T, then the coordinates of T are
a) (0, (4/3)at)
b) (0, 2at)
c) \[\left(\left(1/4\right)at^{2},at\right)\]
d) (0, at)
Explanation: Equation of the line parallel to the axis and

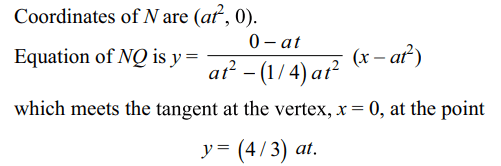
8. If P, Q, R are three points on a parabola
\[y^{2}=4ax\] whose ordinates are in geometrical progression,
then the tangents at P and R meet on
a) the line through Q parallel to x-axis
b) the line through Q parallel to y-axis
c) the line joining Q to the vertex
d) the line joining Q to the focus
Explanation: Let the coordinates of P, Q, R be (ati2 , 2ati)
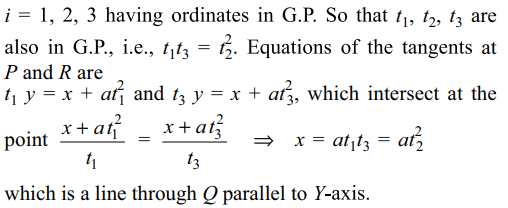
9. The tangents at three points A,B,C on the parabola \[y^{2}=4x\] , taken in pairs intersect at the point
P, Q and R. If \[\triangle ,\triangle ' \] be the areas of the triangles ABC and PQR
respectively, then
a) \[\triangle=2\triangle'\]
b) \[\triangle'=2\triangle\]
c) \[\triangle=\triangle'\]
d) none of these
Explanation: Let the coordinate of A, B, C be (ti 2 , 2ti)

10. The locus of the mid-point of the line segment joining the focus to a moving point on the parabola
\[y^{2}=4ax\] is another parabola with directrix
a) x = – a
b) x = – a/2
c) x = 0
d) x = a/2
Explanation: The focus of the parabola y2 = 4ax is S(a, 0), let