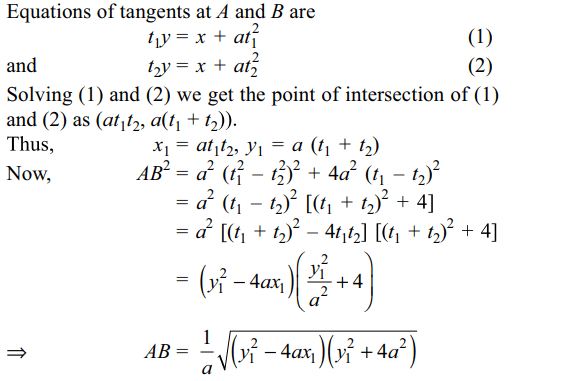1. Equation of a common tangent to the
curves \[y^{2}=8x\] and xy = – 1 is
a) 3y = 9x + 2
b) y = 2x + 1
c) 2y = x + 8
d) y = x + 2
Explanation: Equation of a tangent at (at2 , 2at) to y2 = 8x is ty = x + at2 where 4a = 8 i.e. a = 2
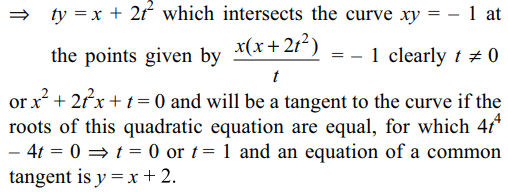
2. The tangent at the point \[P\left(x_{1},y_{1}\right)\] to the parabola \[y^{2}=4ax\] meets the parabola \[y^{2}=4a\] (x + b) at Q
and R, the coordinates of the mid-point of QR are
a) \[\left(x_{1}-a,y_{1}+b\right)\]
b) \[\left(x_{1},y_{1}\right)\]
c) \[\left(x_{1}+b,y_{1}+a\right)\]
d) \[\left(x_{1}-b,y_{1}-b\right)\]
Explanation: Equation of the tangent at P (x1, y1) to the
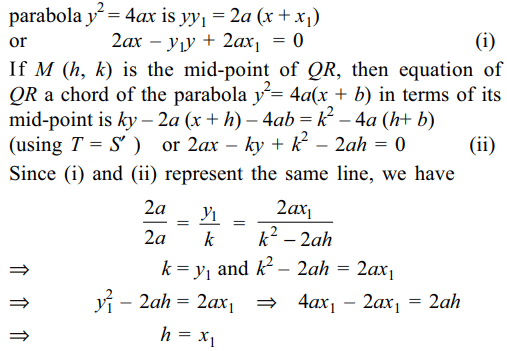
3. Consider a parabola y2 = 4ax, the length
of focal chord is l and the length of the perpendicular from
vertex to the chord is p then
a) l . p is constant
b) \[l p^{2}\] is constant
c) \[l^{2}\] p is constant
d) none of these
Explanation: Let P(at2 , 2at) and Q(a/t2 , –2a/t) be a focal

4. Tangent are drawn to a parabola from a point T. If P, Q are the points of contact, then perpendicular
distance from P, T and Q upon the tangent at the vertex of
the parabola are in
a) A.P
b) G.P
c) H.P
d) none of these
Explanation: Let P(at12 , 2at), Q(at22 , 2at2), then the point of intersection of the tangents t1y = x + at12 and t2y = x + at22 is T(at1t2, a(t1 + t2))
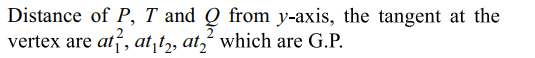
5. Chords of the parabola \[y^{2}+4y=\frac{4}{3}x-\frac{16}{3}\] which subtend right angle at the vertex pass through
a) (7/3, –2)
b) (1/3, 0)
c) (4/3, 0)
d) (0, 4/3)
Explanation: Equation of the parabola is
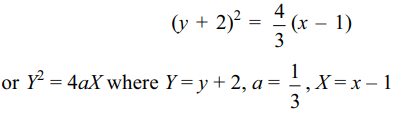
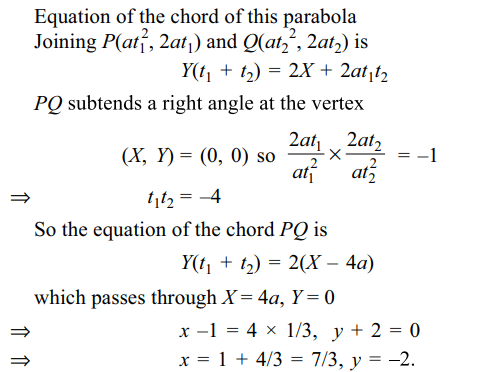
6. The locus of the vertices of the family of parabolas \[y=\frac{a^{3}x^{2}}{3}+\frac{a^{2}x}{2}-2a\]
is
a) \[xy=\frac{105}{64}\]
b) \[xy=\frac{3}{4}\]
c) \[xy=\frac{35}{16}\]
d) \[xy=\frac{64}{105}\]
Explanation: Equation of the parabola is

7. Consider the two curves
\[c_{1}:y^{2}=4x;c_{2}:x^{2} +y^{2} -6x+1\]
then
a) \[c_{1}\] and \[c_{2}\] touch each other only at one point
b) \[c_{1}\] and \[c_{2}\] touch each other exactly at two points
c) \[c_{1}\] and \[c_{2}\] intersect (but do not touch) at exactly two point
d) \[c_{1}\] and \[c_{2}\] neither intersect nor touch each other
Explanation: Solving the two equations, we get
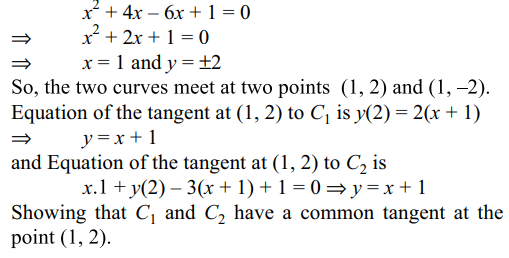

8. If AB is a focal chord of the parabola
\[y^{2}=4ax\] with focus F, then harmonic mean FA and FB is
a) a
b) 2a
c) 4a
d) 8a
Explanation: End points of the focal chord be
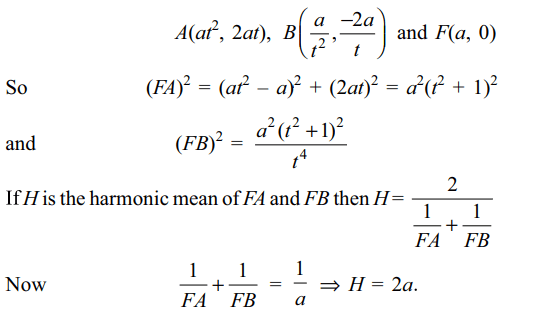
9. Length of the shortest normal chord of
the parabola \[y^{2}=4x\] is
a) 6
b) \[6\sqrt{3}\]
c) 1
d) \[3\sqrt{3}\]
Explanation: Equation of normal to the parabola y2 = 4x at

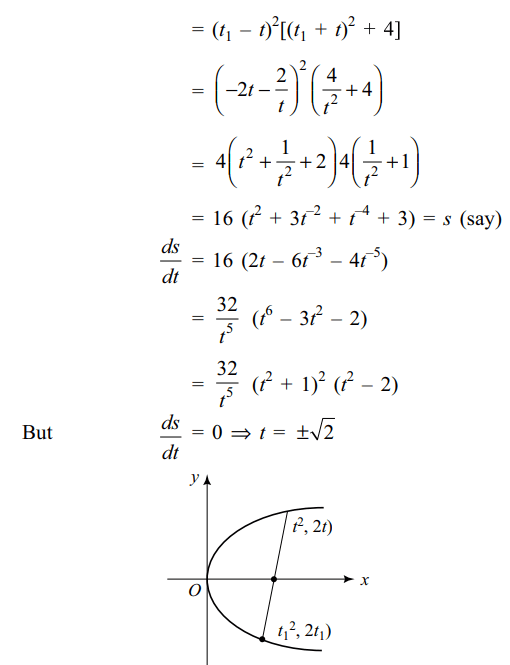
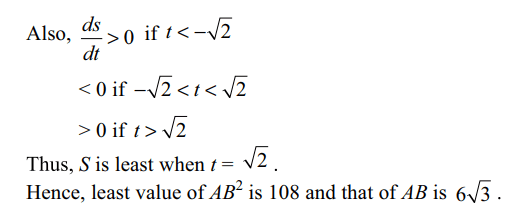
10. Let \[\left(x_{1},y_{1}\right)\] be a point outside the parabola
\[y^{2}=4ax\] . Length of the chord of contact of tangents drawn
from point \[\left(x_{1},y_{1}\right)\] to \[y^{2}=4ax\] is
a) \[\frac{1}{a}\sqrt{\left(y_1^2-4ax_{1}\right)\left(y_1^2+4a^{2}\right)}\]
b) \[\frac{1}{a}\sqrt{\left(y_1^2-4ax_{1}\right)\left(x_1^2+a^{2}\right)}\]
c) \[\frac{1}{a}\sqrt{\left(y_1^2-4ax_{1}\right)\left(x_1^2+4a^{2}\right)}\]
d) \[\frac{1}{a}\sqrt{\left(y_1^2-4ax_{1}\right)\left(y_1^2+a^{2}\right)}\]
Explanation: Let the tangets at the point A (at1 2 , 2at1) and B(at22,2at2) pass through (x1, y1) ,