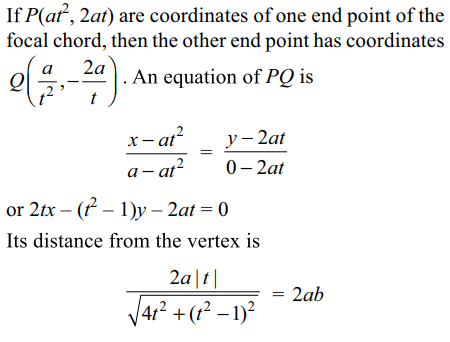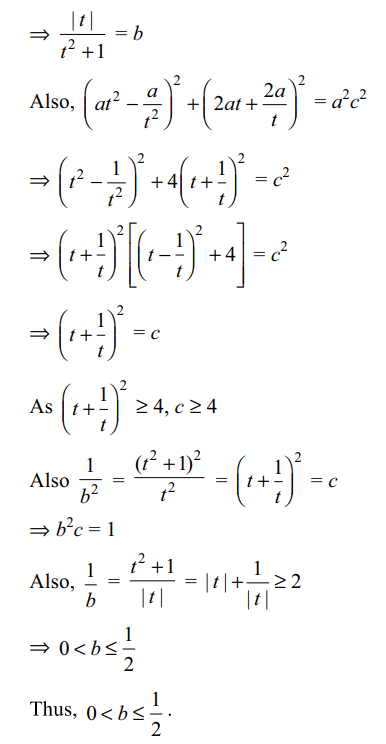1. Equation of the normal at a point on the parabola \[y^{2}=36x\] , whose ordinate is three times its abscissa is
a) 2x + 3y + 44 = 0
b) 2x – 3y + 44 = 0
c) 2x + 3y – 44 = 0
d) 2x – 3y = 0
Explanation:

2. If a,b> 0 , then the angle of intersection of two
parabolas \[y^{2}=a^{3}x\] and \[x^{2}=b^{3}y\] at a point other than
the origin is
a) \[\tan^{-1}\left(\frac{3ab}{2\left(a^{2}+b^{2}\right)}\right)\]
b) \[\tan^{-1}\left(\frac{ab}{\left(a^{2}+b^{2}\right)}\right)\]
c) \[\tan^{-1}\left(\frac{a^{2}+b^{2}}{ab}\right)\]
d) \[\tan^{-1}\left(\frac{3\left(a^{2}+b^{2}\right)}{2ab}\right)\]
Explanation:

3. O is the vertex and LL' is the latus rectum of the parabola.
Let P be a point on the parabola and Q be a point on the axis of the parabola such that \[ OPQ =\frac{\pi}{2}.\] Suppose length of the projection of
PQ on the axis of the parabola be \[\alpha\] , then \[\alpha -\mid LL'\mid\] equals
a) a
b) 2a
c) -a
d) 0
Explanation:
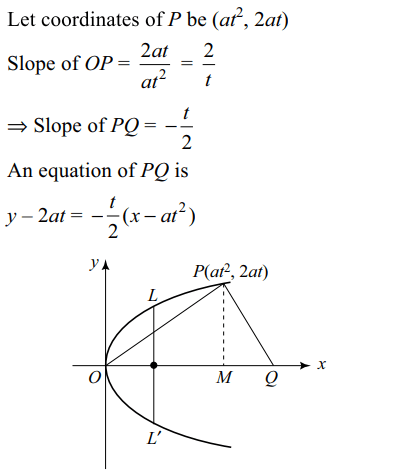
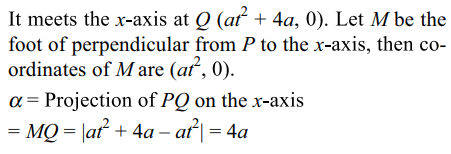

4. An equation of the latus rectum of the parabola \[x^{2}+4x+2y=0\] is
a) \[y=-\frac{3}{2}\]
b) \[y=\frac{2}{3}\]
c) \[y=\frac{3}{2}\]
d) \[y=-\frac{2}{3}\]
Explanation:
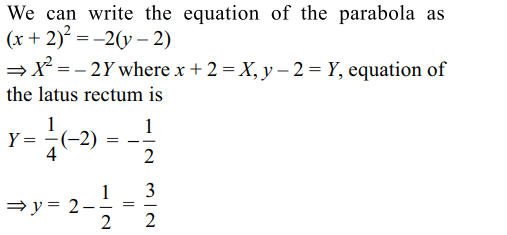
5. \[y=\left(x-11\right) \cos\theta-\cos3\theta\] is a normal to the parabola
\[y^{2}=16x\] for
a) only one value of \[\theta\]
b) two values of \[\theta\]
c) all values of \[\theta\]
d) no value of \[\theta\]
Explanation:

6. If the normals are drawn from the point P(5, b) to
the parabola \[y^{2}=4x\] , then
a) there are three normal if –2 < b < 2
b) there id exactly one normal with positive
slope if b< -2
c) there is exactly one normal with negative slope if b > 2
d) All of the Above
Explanation:
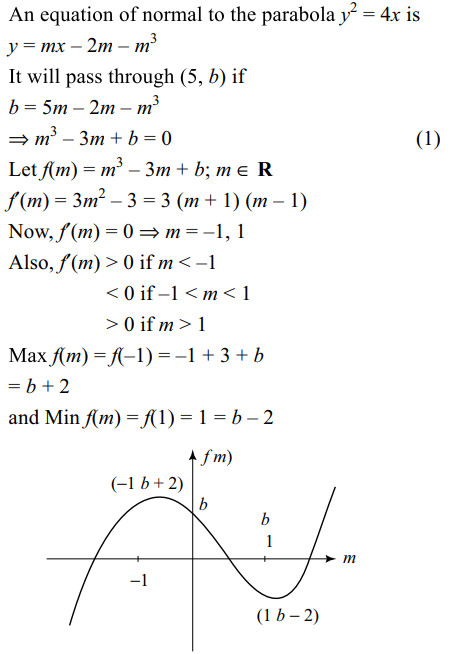

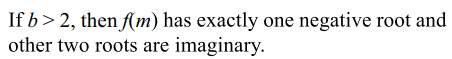
7. Equations (s) of the commom tangent (s) to the parabola and \[y^{2}=4x\] is \[x^{2}+4y^{2}=8\] are
a) x + 2y + 4 = 0
b) x + 2y – 4 = 0
c) x – 2y – 4 = 0
d) Both a and c
Explanation:
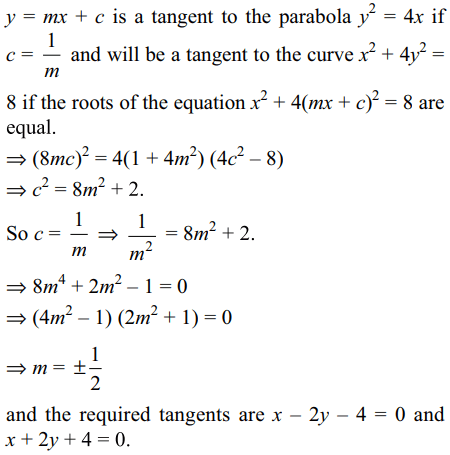
8. A circle with centre (a,0) touches the directrix of
the parabola \[y^{2}=4ax.\] Tangents to the parabola at
points of intersection of the parabola and the circle are.
a) x + y + a = 0
b) x + y – a = 0
c) x – y + a = 0
d) Both a and c
Explanation:

9. The points of contact of tangents from (-3,5) to the parabola \[y^{2}=4\left(x-3\right)\] are
a) (4, 2)
b) (4, –2)
c) (39, 12)
d) Both b and c
Explanation:
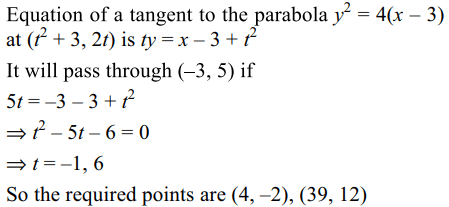
10. If length of focal chord of the parabola \[y^{2}=4ax\] at a
distance 2ab from the vertex is ac, then
a) \[0< b\leq\frac{1}{2}\]
b) \[c\geq 4\]
c) \[b^{2}c=1\]
d) Both a and c
Explanation: