1. A speaks the truth in 70 percent cases and B in
80 percent cases. The probability that they will
contradict each other in describing a single event is
a) 0.36
b) 0.38
c) 0.4
d) 0.42
Explanation:
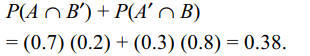
2. 2n boys are randomly divided into two subgroups
containing n boys each. The probability that the two
tallest boys are in different groups is
a) \[\frac{n}{2n-1}\]
b) \[\frac{n-1}{2n-1}\]
c) \[\frac{2n-1}{4n^{2}}\]
d) \[\frac{n-1}{2n^{2}}\]
Explanation:
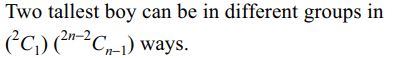
3.The numbers 1, 2, 3, .... , n are arranged in random
order. The probability that the digits 1, 2, .... , k (k <
n) appears as neighbours in that order is
a) \[\frac{1}{n!}\]
b) \[\frac{k!}{n!}\]
c) \[\frac{\left(n-k\right)!}{n!}\]
d) \[\frac{\left(n-k+1\right)!}{n!}\]
Explanation: 1, 2, 3, .... k appear together in that order in (n - k + 1)! ways
4. Two boys and three girls stand in a queue. The probability
the number of boys ahead of every girl is at
least one more than the number of girls ahead of her
a) 1/2
b) 1/3
c) 2/3
d) 0
Explanation: Impossible event
5. A bag contains some white and some black balls,
all combinations of balls being equally likely. The
total number of balls in the bag is 10. If three balls
are drawn at random without replacement and all of
them are found to be black, the probability that the
bag contains 1 white and 9 black balls is
a) 14/55
b) 12/55
c) 2/11
d) 8/55
Explanation:
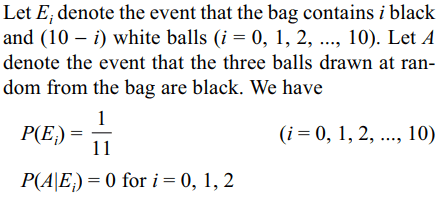
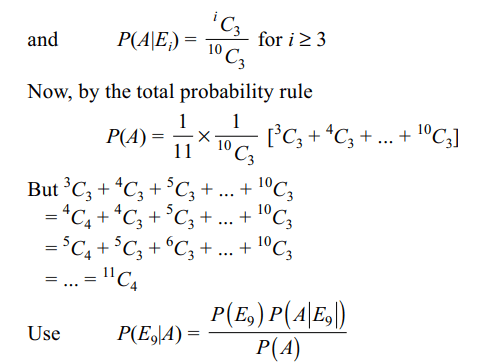
6. Let E, F, G be pairwise independent events with
P (G) > 0 and \[P\left(E\cap F\cap G\right)=0\] . Then \[P\left(E'\cap F' \mid G\right)\] equals
a) \[P\left(E'\right)+P\left(F'\right)\]
b) \[P\left(E'\right)-P\left(F'\right)\]
c) \[P\left(E'\right)-P\left(F\right)\]
d) \[P\left(E\right)-P\left(F'\right)\]
Explanation:
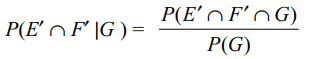
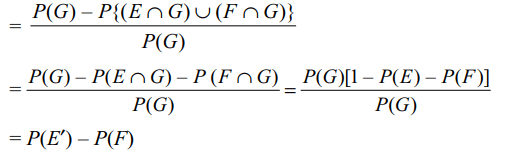
7. A and B are two events. The probability that at most
one of A, B occurs is
a) \[1-P\left(A\cap B\right)\]
b) \[P\left(A'\right)+P\left(B'\right)-P\left(A'\cap B'\right)\]
c) \[P\left(A'\right)+P\left(B'\right)+P\left(A\cup B\right)-1\]
d) All of the Above
Explanation: All of the Above
8. The probability of the simultaneous occurrence
of two events A and B is p. If the probability that
exactly one of A, B occurs is q, then
a) \[P\left(A'\right)+P\left( B'\right)=2-2p-q\]
b) \[P\left(A\cap B \mid A\cup B\right)=\frac{p}{p+q}\]
c) \[P\left(A'\cap B' \right)=1-p-q\]
d) All of the Above
Explanation: All of the Above
9. Suppose that P(A) = 3/5 and P(B) = 2 3. Then
a) \[P\left(A\cup B \right)\geq 2/3\]
b) \[4/15 \leq P\left(A\cap B \right)\leq 3/5\]
c) \[2/5 \leq P\left(A\mid B \right)\leq 9/10\]
d) All of the Above
Explanation: All of the Above
10. If E and F are independent events such that
0 < P(E) < 1 and 0 < P(F) < 1, then
a) E and F' are independent
b) E' and F' are independent
c) P(E|F) + P(E' | F) = 1
d) All of the Above
Explanation: All of the Above