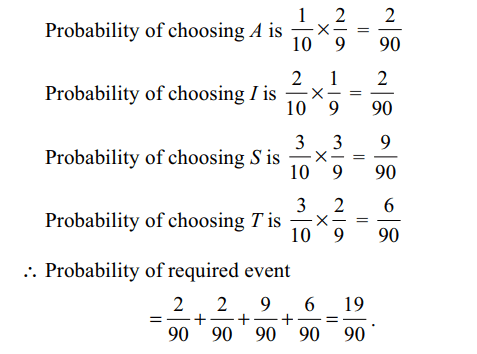1. One hundred identical coins, each with
probability p of showing heads are tossed once. If 0 < p <
1 and the probability of heads showing on 50 coins is equal
to that of heads showing on 51 coins, the value of p is
a) 1/2
b) 51/101
c) 49/101
d) 3/101
Explanation: Let X be the number of coins showing heads. Then X follows a binomial distribution with parameters n
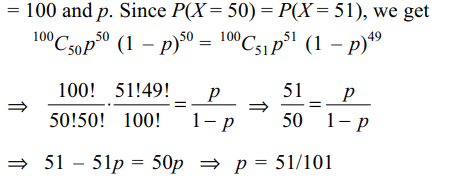
2. Suppose X follows a binomial distribution
with parameters n and p, where 0 < p < 1.If P(X = r)/P(X = n – r) is independent of n for every value
of r, then
a) p = 1/2
b) p = 1/3
c) p = 1/4
d) p = 1/5
Explanation:
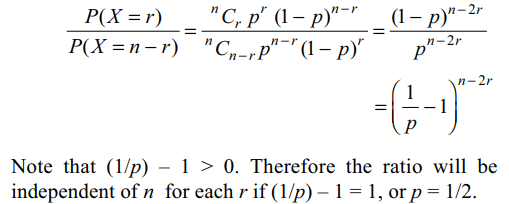
3. The minimum number of times a fair
coin must be tossed so that the probability of getting at
least one head is at least 0.8 is
a) 7
b) 6
c) 5
d) 3
Explanation: Suppose the coin is tossed n times. Let X be the number of heads obtained. Then X follows a binomial distribution with parameters n and p = 1/2. We have P(X≥ 1) ≥ 0.8 \[\Rightarrow\] 1 – P(X = 0) ≥ 0.8
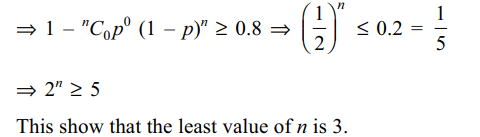
4. For the three events A, B and C,
P (exactly one of the events A or B occurs) = P(exactly
one of the events B or C occurs) = P(exactly one of the
events C or A occurs) = p and P(all the three events
occur simultaneously) = \[p^{2}\], where 0 < p < 1/2. Then the
probability of at least one of the three events A, B and C
occurring is
a) \[\frac{3p+2p^{2}}{2}\]
b) \[\frac{p+3p^{2}}{4}\]
c) \[\frac{p+3p^{2}}{2}\]
d) \[\frac{3p+2p^{2}}{4}\]
Explanation:
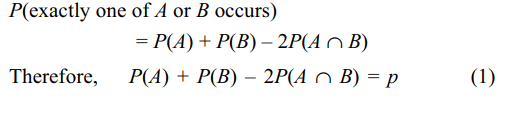
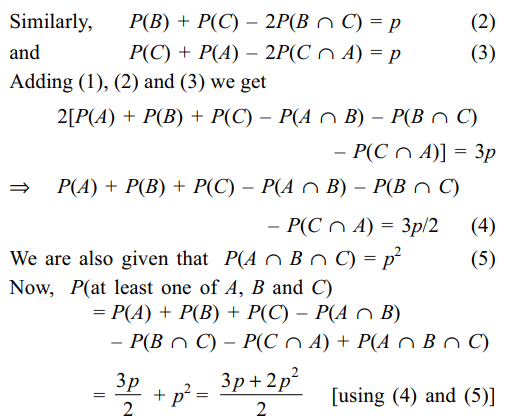
5. Nine identical balls are numbers 1, 2,
...9. are put in a bag. A draws a ball and gets the number
a. The ball is put back the bag. Next B draws a ball gets
the number b. The probability that a and b satisfics the
inequality a – 2b + 10 > 0 is
a) \[\frac{52}{81}\]
b) \[\frac{55}{81}\]
c) \[\frac{61}{81}\]
d) \[\frac{62}{81}\]
Explanation: a – 2b + 10 > 0
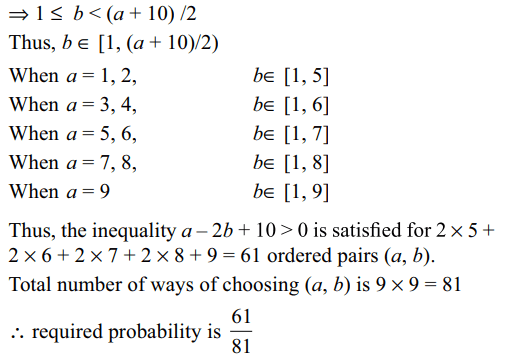
6. An unbiased die with faces marked 1, 2,
3, 4, 5 and 6 is rolled four times. Out of four face values
obtained, the probability that the minimum face value is
not less than 2 and the maximum face value is not greater
than 5 is
a) 16/81
b) 1/81
c) 80/81
d) 65/81
Explanation:
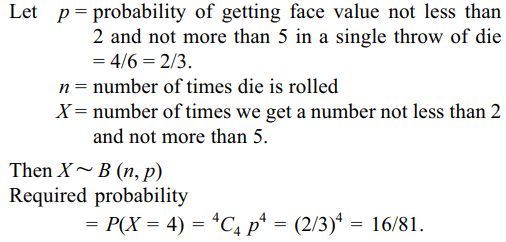
7. If the papers of 4 students can be checked
by any one of the 7 teachers, then the probability that all the
4 papers are checked by exactly 2 teachers is
a) 2/7
b) 6/49
c) 32/343
d) 1/7
Explanation: The total number of ways in which papers of 4

8. Let A, B,C, be three mutually independent
events. Consider the two statements \[S_{1}\] and \[S_{2}\]
\[S_{1} : A\] and B \[\cup C\] are independent
\[S_{2} : A\] and B \[\cap C\] are independent
Then
a) Both \[S_{1}\] and \[S_{2}\] are true
b) Only \[S_{1} \] is true
c) Only S2 is true
d) Neither \[S_{1}\] nor \[S_{2}\] is true
Explanation:
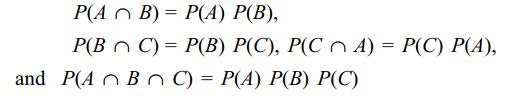

9. If m is a natural such that \[m \leq 5\] , then the
probability that the quadratic equation \[x^{2}+mx+\frac{1}{2} +\frac{m}{2}=0\]
has real roots is
a) 1/5
b) 2/3
c) 3/5
d) 1/5
Explanation: Discriminant D of the quadratic equation
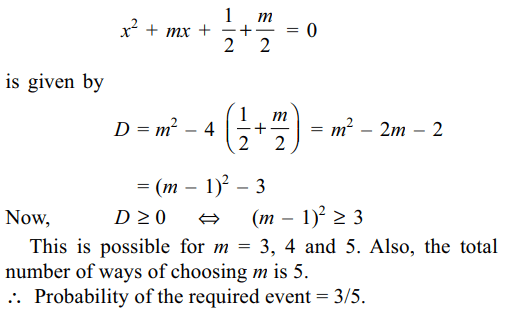
10. A letter is taken at random from the letters
of the word ‘STATISTICS’ and another letter is taken at
random from the letters of the word ‘ASSISTANT’. The
probability that they are the same letter is
a) 1/45
b) 13/90
c) 19/90
d) 5/18
Explanation: Letters of the word STATISTICS are