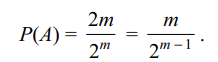1. Suppose X ~ B(n, p) and P(X = 3) = P(X = 5). If p >
1/2, then
a) \[ n\leq 7\]
b) n > 8
c) \[n\geq 9\]
d) \[n\geq 10\]
Explanation:
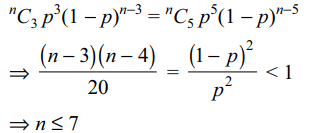
2. In three throw of a pair dice, the probability throwing
doublets not more than twice is
a) 1/6
b) 5/72
c) 215/216
d) 7/128
Explanation:
3. A bag contains 4 brown and 5 white socks. A man
pulls two socks at random without replacement. The
probability that the man gets both the socks of the
same colour is
a) 5/108
b) 1/6
c) 5/18
d) 4/9
Explanation:
4. A is a set containing n elements. Two subsets P
and Q of A are chosen at random. (P and Q may
have elements in common). The probability that
\[P\cup Q\neq A\] is
a) \[\left(3/4\right)^{n}\]
b) 1/4n
c) \[^{n}C_{2}/2^{n}\]
d) \[1-\left(3/4\right)^{n}\]
Explanation:
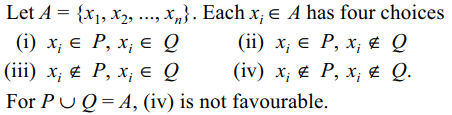
5. Three of the six vertices of a regular hexagon are
chosen at random. The probability that the triangle
with these vertices is not equilateral is
a) 1/2
b) 1/5
c) 9/10
d) 1/20
Explanation: Find probability of the complement event.
9/10
6. A positive integer is chosen at random. The
probability that the sum of the digits of its square is
39 is
a) 1/39
b) 2/39
c) 1/11
d) 0
Explanation:
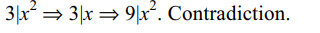
7. A lottery sells \[n^{2}\] tickets and declares n prizes. If
a man purchases n tickets, the probability of his
winning at least one prize is
a) \[\left(n^{2}-n\right)!/\left(n^{2}\right)!\]
b) 1/2n
c) \[\left(n-1\right)!^{2}/\left(n^{2}\right)!\]
d) none of these
Explanation:
8. Let x be a non-zero real number. A determinant is
chosen from the set of all determinants of order 2
with entries x or – x only. The probability that the
value of the determinant is non-zero is
a) 3/16
b) 1/4
c) 1/2
d) 1/8
Explanation:
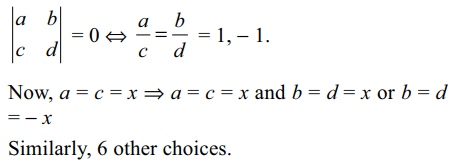
9. A die is rolled three times. The probability of getting a
number larger than the previous number each time is
a) 5/72
b) 5/54
c) 13/216
d) 1/18
Explanation:
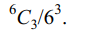
10. In a game called “odd man out man out,”
m (m > 2) persons toss a coin to determiane
who will buy refreshments for the entire group.
A person who gets an outcome different from that
of the rest of the members of the group is called the
odd man out. The probability that there is a loser in
any game is
a) 1/2m
b) \[m/2^{m-1}\]
c) 2/m
d) \[1/2^{m-1}\]
Explanation: