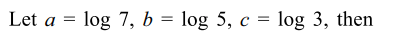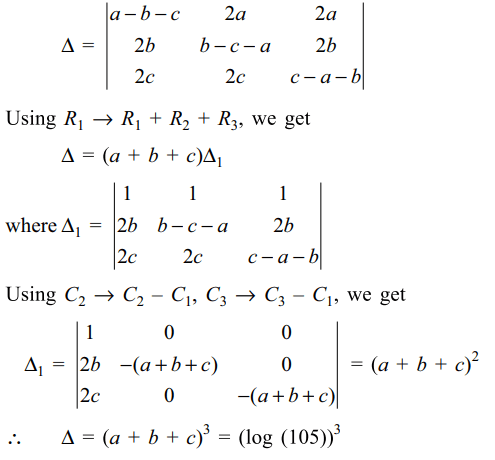1. The value of \[\frac{\log_{2}24}{\log_{96}2}-\frac{\log_{2}192}{\log_{12}2}\]
is
a) 3
b) 0
c) 2
d) 1
Explanation:
2. The set of all value of x satisfying \[x^{\log_{x}\left(1-x\right)^{2}}=9\]
is
a) a subset of R containing N
b) a subset of R containing 1
c) is a finite set containg at least two elements
d) a finite set .
Explanation: Note that x > 0, x \[\neq\] 1
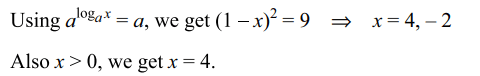
3. The set \[\left\{x: \mid 1-\log_{1/5}x\mid +2=\mid 3-\log_{1/5}x\mid\right\}\] is equal to
a) \[\left( 0,\infty\right)\]
b) \[\left[ 1/5,\infty\right)\]
c) \[\left[ 1/5,5\right)\]
d) \[\left(0,1/5\right]\]
Explanation:
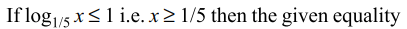
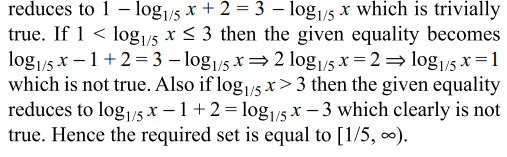
4. The set of \[\left\{x: \log_{1/3}\log_{4}\left(x^{2}-5\right)>0\right\}\] is equal to
a) \[\left(3,\infty\right)\]
b) \[\left(\sqrt{6},3\right)\]
c) \[\left(-3,-\sqrt{6}\right)\cup\left(\sqrt{6},3\right)\]
d) \[\left(\sqrt{6},\infty\right)\]
Explanation:
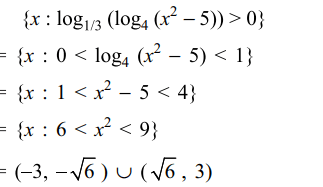
5. The number of solutions of \[\log_{4}\left(x-1\right)=\log_{2}\left(x-3\right)\]
is
a) 3
b) 1
c) 2
d) 0
Explanation:

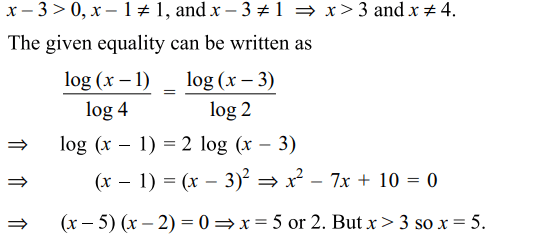
6. Solutions set of the inequality
\[\log_{3}\left(x+2\right)\left(x+4\right)+\log_{1/3}\left(x+2\right)<\frac{1}{2}\log_{\sqrt{3}}7\]
is
a) \[\left(-2,-1\right)\]
b) \[\left(-2,3\right)\]
c) \[\left(-1,3\right)\]
d) \[\left(3,\infty\right)\]
Explanation:
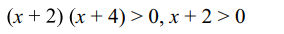
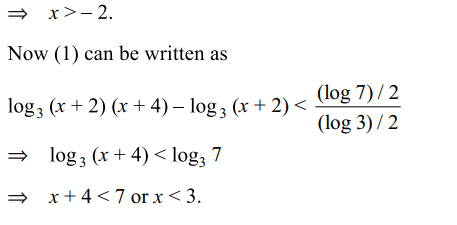
7. The solution set of \[\log_{\mid\sin x\mid}\left(x^{2}-8x+23\right)>\frac{3}{\log_2{\mid\sin x\mid}}\] contains
a) \[x\epsilon \left(3,\pi\right)\cup\left(\pi,\frac{3\pi}{2}\right)\cup\left(\frac{3\pi}{2},5\right)\]
b) \[x\epsilon \left(3,\pi\right)\cup\left(\pi,5\right)\]
c) \[x\epsilon \left(3,\frac{5\pi}{2}\right)\]
d) \[x\epsilon \left(2,5\pi/2\right)\]
Explanation:
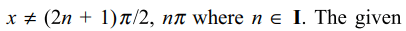
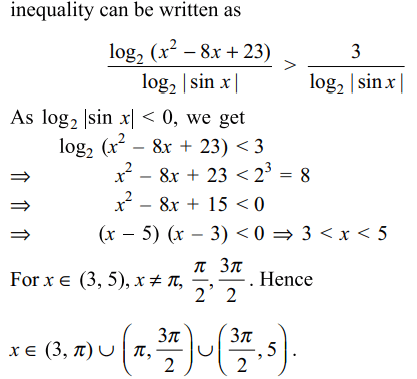
8. If n>1, the value of \[\frac{1}{\log_{2}n}+\frac{1}{\log_{3}n}+....+\frac{1}{\log_{53}n}\]
is
a) \[\frac{1}{\log_{53!}n}\]
b) 1
c) \[\frac{1}{\log_{n!}53}\]
d) \[\frac{1}{53}\]
Explanation:
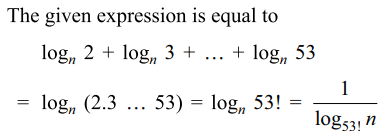
9. The number of values of \[x \epsilon \left[0,n\pi\right],n \epsilon I\] that satisfy
\[\log_{\mid \sin x\mid}\left(1+\cos x\right)=2\] is
a) 0
b) n
c) 2n
d) 1
Explanation:
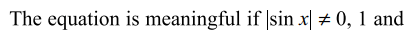
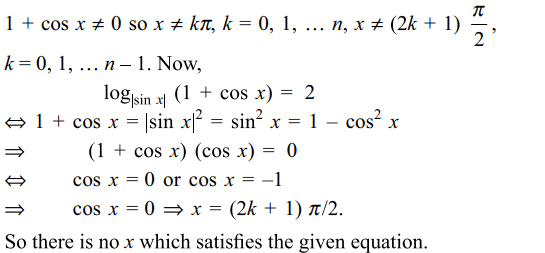
10. Let \[\triangle=\begin{bmatrix}\log \left(7/15\right) & \log \left(49\right) & \log \left(49\right) \\\log \left(25\right) &\log \left(5/21\right) & \log \left(25\right) \\\log \left(9\right) & \log \left(9\right) &\log \left(3/35\right)\end{bmatrix}\]
then \[\triangle\] is equal to
a) \[\left(\log \left(105\right)\right)^{2}\]
b) \[\left(\log \left(105\right)\right)^{3}\]
c) \[\left(\log \left(35/3\right)\right)^{3}\]
d) \[\left(\log \left(21/5\right)\right)^{3}\]
Explanation: