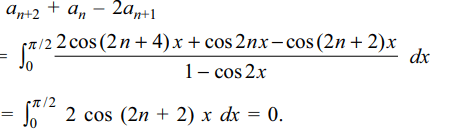1. If \[a_{1},a_{2},...,a_{n}\] are in H.P., then
\[\frac{a_{1}}{a_{2}+a_{3}+....+a_{n}},\frac{a_{2}}{a_{1}+a_{3}+....+a_{n}},....\frac{a_{n}}{a_{1}+a_{2}+....+a_{n-1}}\]
are in
a) A.P
b) H.P
c) G.P
d) A.G.P.
Explanation:
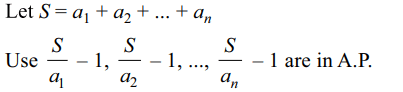
2.Let \[S_{n}=\sum_{r=1}^{n}t_{r}=\frac{1}{6}n\left(2n^{2}+9n+13\right) ,then \sum_{r=1}^{n}\sqrt{t_{r}}\]
equals
a) \[\frac{1}{2}n\left(n+1\right)\]
b) \[\frac{1}{2}n\left(n+3\right)\]
c) \[\left(n+1\right)^{2}\]
d) \[n^{2}\]
Explanation:
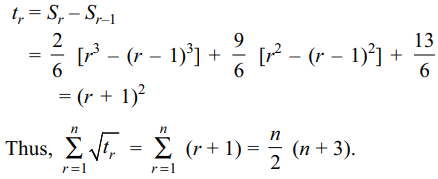
3. Let \[a_{n}=\underbrace{111.......1}_{n }\]
. The remainder when \[a_{124}\] is divided by 271 is
a) 23
b) 25
c) 27
d) 29
Explanation:
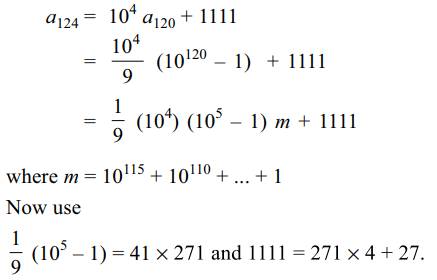
4. Three arithmetic means, three geometric means and
three harmonic means are inserted between 1 and 5.
The cubic equation whose roots are 3rd A.M., 2nd
G.M. and 1st H.M. is
a) \[x^{3}-\frac{1}{4}\left(21+4\sqrt{5}\right)x^{2}+5x-5\sqrt{5}=0\]
b) \[x^{3}-\frac{1}{4}\left(21+4\sqrt{5}\right)x^{2}+\left(5+\frac{21}{4}\sqrt{5}\right)x-5\sqrt{5}=0\]
c) \[4x^{3}-\left(21+4\sqrt{5}\right)x^{2}+\left(15+21\sqrt{5}\right)-20\sqrt{5}=0\]
d) none of these
Explanation:
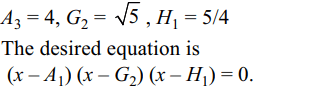
5. If \[t_{r}\] denotes the rth term of an A.P., and tp = 1/q,
\[t_{q}=1/p\] then which of the following is a root of the
equation \[\left(p + 2q + 3r\right) x^{2} + \left(q + 2r – 3p\right) x +\left(r + 2p – 3q\right) = 0\]
a) \[t_{p}\]
b) \[t_{q}\]
c) \[t_{pq}\]
d) \[t_{p+q}\]
Explanation: Clearly 1 is a root of the equation and tpq = 1
6. If the pth term of an A.P. is 1/q and qth term is 1/p
and sum of pq terms is 25pq, then p and q are connected
by
a) \[p^{2}=4q^{2}+1\]
b) p = 4q – 1
c) pq = 4 + p
d) pq = 25
Explanation:
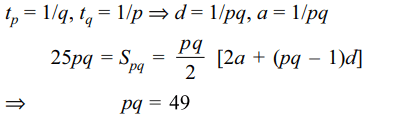
7. If \[p\left(x\right)=\frac{1+x^{2}+x^{4}+...+x^{2n-2}}{1+x+x^{2}+....+x^{n-1}}\]
is a polynomial in x, then n must be
a) odd
b) even
c) greater than 5
d) less than 5
Explanation:

8. \[\sqrt{\underbrace{111......1}_{200 digit }-\underbrace{222.....2}_{100 digit }}\] equals
a) \[\sqrt{\underbrace{1313......13}_{100 digit }}\]
b) \[\sqrt{\underbrace{33......3}_{100 digit }}\]
c) \[\sqrt{\underbrace{2323......23}_{100 digit }}\]
d) none of these
Explanation:
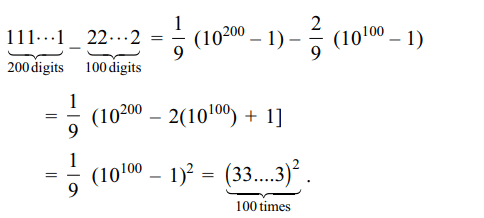
9. Let \[S_{n}\left(a\right)=1+2\left(1-a\right)+3\left(1-a\right)\left(1-2a\right)+4\left(1-a\right)\left(1-2a\right)\left(1-3a\right)+....\]
upto n terms, then \[S_{100}\left(\frac{1}{99}\right)\] equals
a) 100/99
b) 1/99
c) 200
d) 99
Explanation:
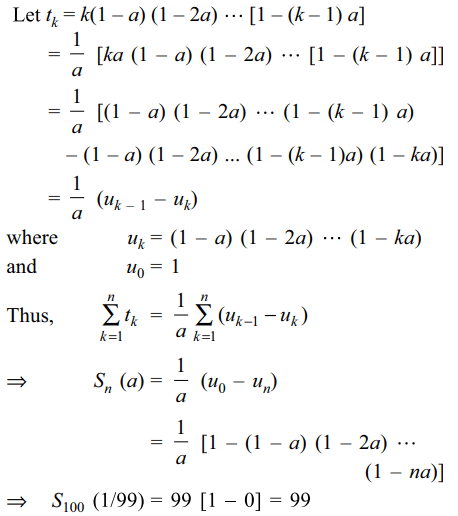
10. Let \[a_{n}=\int_{0}^{\pi/2} \frac{1-\cos2n x}{1-\cos2x}dx\] then \[a_{1},a_{2},a_{3}...\] are in
a) A.P
b) G.P
c) H.P
d) none of these
Explanation: