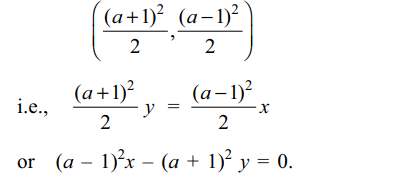1. A rectangle ABCD, A = (0, 0), B =
(4, 0), C = (4, 2), D = (0, 2) undergoes the following
transformations successively.\[\left(i\right)f_{1}\left(x,y\right)\rightarrow\left(y,x\right)\left(ii\right)f_{2}\left(x,y\right)\rightarrow\left(x+3y,y\right),\left(iii\right)f_{3}\left(x,y\right)\rightarrow\left(\frac{x-y}{2},\frac{x+y}{2}\right)\]
The final fingure will be
a) a square
b) a rhombus
c) a rectangle
d) a parallelogram
Explanation: A remains (0, 0)
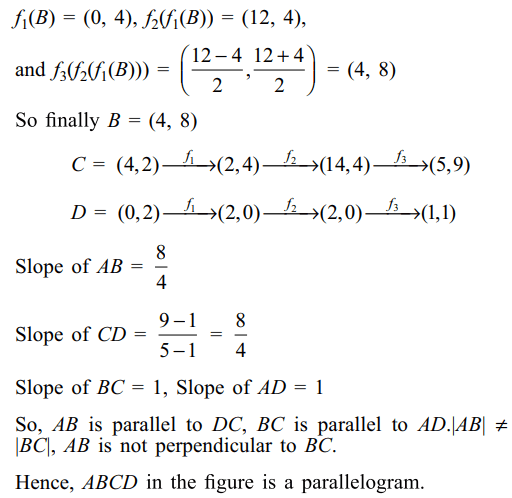
2. A straight line L through the point (3,
–2) is inclined at an angle 60° to the line \[\sqrt{3}x+y=1\] .
If L also intersects the x-axis, then the equation of L is
a) \[y+\sqrt{3}x+2-3\sqrt{3}=0\]
b) \[y-\sqrt{3}x+2+3\sqrt{3}=0\]
c) \[\sqrt{3}y-x+2\sqrt{3}=0\]
d) \[\sqrt{3}y+x-3+2\sqrt{3}=0\]
Explanation: Let m be the slope of required line, then
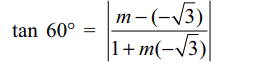
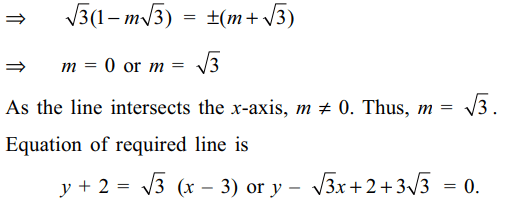
3. Let P = (– 1, 0), Q = (0, 0) and \[R=\left(3,3\sqrt{3}\right)\] be three points. Then the equation of the bisector of
the angle PQR is
a) \[\left(\sqrt{3}/2\right)x+y=0\]
b) \[x+\sqrt{3}y=0\]
c) \[\sqrt{3}x+y=0\]
d) \[x+\left(\sqrt{3}/2\right)y=0\]
Explanation:
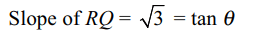

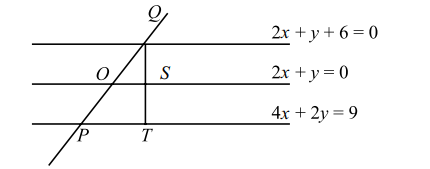
4. A straight line through the origin O meets
the parallel lines 4x + 2y = 9 and 2x + y + 6 = 0 at points P
and Q respectively. Then the point O divides the segment
PQ in the ratio.
a) 1 : 2
b) 3 : 4
c) 2 : 1
d) 4 : 3
Explanation: Equation of the line through O parallel to the given lines is 2x + y = 0. Let QST be perpendicular to these lines
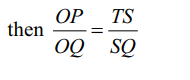
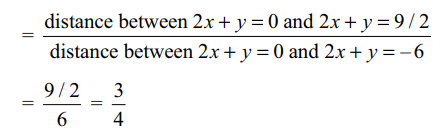
5. Let \[A_{0}A_{1}A_{2}A_{3}A_{4}A_{5}\] be a regular hexagon
inscribed in a circle of unit radius. Then the product of the
length of the line segments \[A_{0}A_{1},A_{0}A_{2}\] and \[A_{0}A_{4}\] is
a) 3/4
b) \[3\sqrt{3}\]
c) 3
d) \[3\sqrt{3}/2\]
Explanation: Let OAO = 1
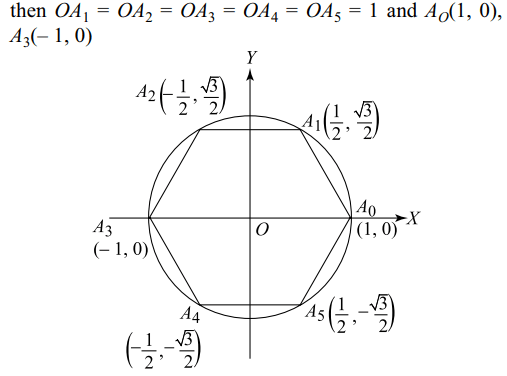
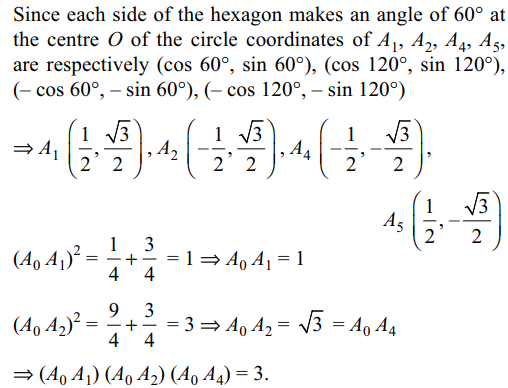
6. The diagonals of a parallelogram PQRS
are along the lines x + 3y = 4 and 6x – 2y = 7, then PQRS
must be a
a) rectangle
b) square
c) cyclic quadrilateral
d) rhombus
Explanation: Since the diagonals intersect at right angles, PQRS is a rhombus.
7. The orthocentre of the triangle formed by
the lines xy = 0 and x + y = 1 is
a) (1/2, 1/2)
b) (1/3, 1/3)
c) (0, 0)
d) (1/4, 1/4)
Explanation: Since the triangle is right angled formed by the line x = 0, y = 0 and x + y = 1 the orthocentre lies at the vertex (0, 0), the point of intersection of the perpendicular lines x = 0 and y = 0
8. The straight lines x + y = 0, 3x + y – 4 =
0, x + 3y – 4 = 0 form a triangle which is
a) isosceles
b) equilateral
c) right angled
d) none of these
Explanation: Vertices of the triangle are
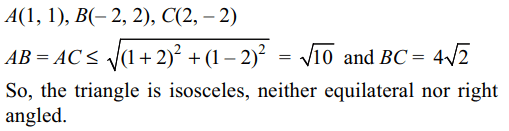
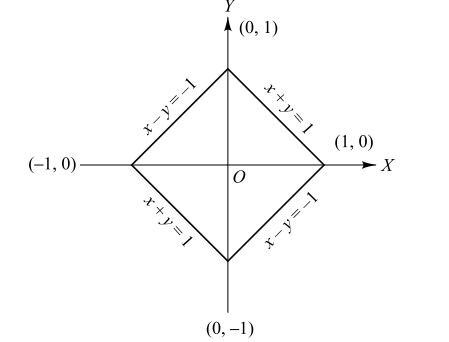
9.If sum of the distances of a point from
two perpendicular lines in a plane is 1, then its locus is
a) a square
b) a circle
c) a straight line
d) two intersecting lines
Explanation: Let the two perpendicular lines be taken as the coordinate axes. If (h, k) be any point on the locus, then according to the given condition | h | + | k | = 1
locus of (h, k) is | x | + | y | = 1
This consists of four line segments which enclose a square
10. If the circumcentre of a triangle lies at
the origin and centroid is the middle point of the line
joining the points \[\left(a^{2}+1,a^{2}+1\right)\] and (2a, – 2a), then the
orthocentre lies on the line.
a) \[y=\left(a^{2}+1\right)x\]
b) y = 2ax
c) x + y = 0
d) \[\left(a-1\right)^{2}x-\left(a+1\right)^{2}y=0\]
Explanation: We know from geometry that the circumcentre, centroid and orthocentre of a triangle lie on a line. So the orthocentre of the triangle lies on the line joining the circumcentre (0, 0) and the centroid