1. A square with each side equal to a lies
above the x-axis and has one vertex at the origin. One of
the sides passing through the origin makes an angle
\[\alpha \left(0< \alpha <\pi/4\right)\] with the positive direction of the x-axis.
Equation of a diagonal of the square is
a) \[y \left(\cos \alpha-\sin \alpha \right)=x\left(\sin\alpha+\cos\alpha\right)\]
b) \[y \left(\sin\alpha+\cos \alpha \right)+x\left(\cos\alpha-\sin\alpha\right)=a\]
c) \[x \left(\cos \alpha-\sin \alpha \right)=y\left(\cos\alpha+\sin\alpha\right)\]
d) Both a and b
Explanation: Let the side OA make an angle \[\alpha\] with the x-axis. Then the coordinates of A are (a cos \[\alpha\] , a sin \[\alpha\] ). Also, the diagonal OB makes an angle \[\alpha\] + \[\pi\] /4 with the x-axis, so that its equation is

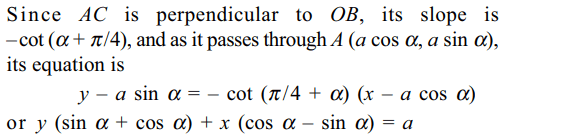
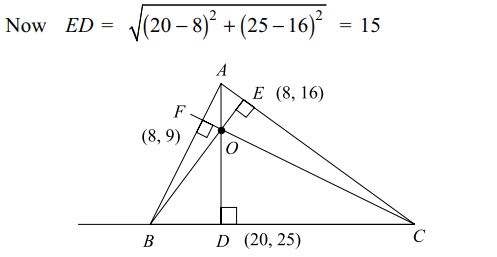
2. The coordinates of the feet of the perpendiculars
from the vertices of a triangle on the opposite sides
are (20, 25), (8, 16) and (8, 9). The coordinates of a vertex
of the triangle are
a) (5, 10)
b) (50, -5)
c) (15, 30)
d) All of the Above
Explanation: We use the fact that the orthocentre O of the triangle ABC is the incentre of the pedal triangle DEF. Let (h, k) be the coordinates of O.
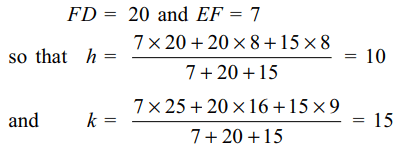
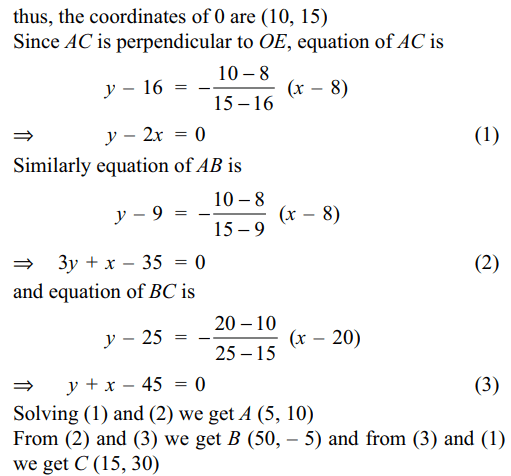
3.If the area of the triangle formed by the
lines y = x, x + y = 2 and the line through P(h, k) and
parallel to x-axis is \[4h^{2}\], the locus of P can be
a) 2x – y + 1 = 0
b) 2x + y – 1 = 0
c) x – 2y + 1 = 0
d) Both a and b
Explanation: Coordinates of A are (1, 1) which is the point of intersection of the given lines. y = k is the line through P parallel to x-axis which meets the given lines at B and C. So coordinates of B are (k, k) and C are (2 – k, k).
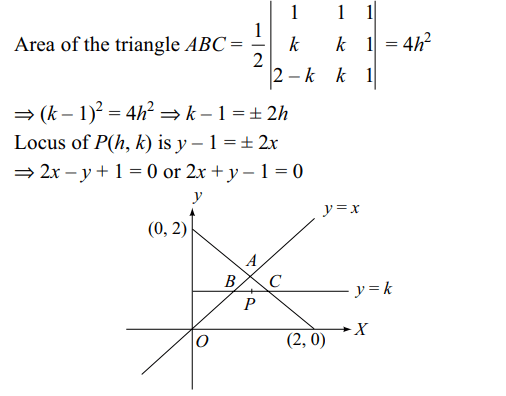
4.Let S be a square with unit area. Consider
any quadrilateral which has one vertex on each side of S. If
a, b, c, d denote the lengths of the sides of the quadrilateral,
then \[\alpha \leq a^{2}+b^{2}+c^{2}+d^{2}\leq\beta\] where
a) \[\alpha=1\]
b) \[\beta=4\]
c) \[\alpha=2\]
d) Both b and c
Explanation: Let the squares of unit area be bounded by the

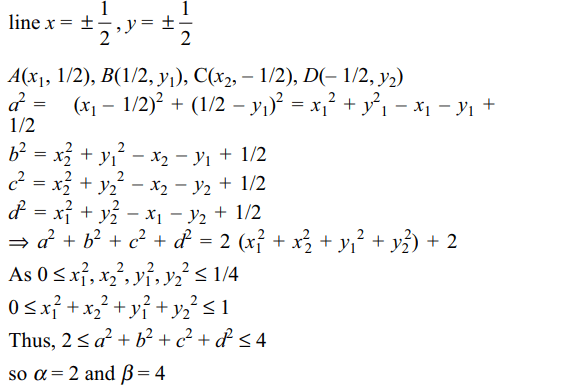
5. Three lines px + qy + r = 0, qx + ry + p =
0 and rx + py + q = 0 are concurrent if
a) p + q + r = 0
b) \[p^{2}+q^{2}+r^{2}=pq+qr+rp\]
c) \[p^{3}+q^{3}+r^{3}=3pqr\]
d) All of the Above
Explanation:

6. An equation of a straight line passing
through the point (2, 3) and having an intercept of length
2 units between the straight lines 2x + y = 3, 2x + y = 5 is
a) x – 2 = 0
b) y – 3 = 0
c) 3x + 4y – 18 = 0
d) Both a and c
Explanation: Any line through (2, 3) is
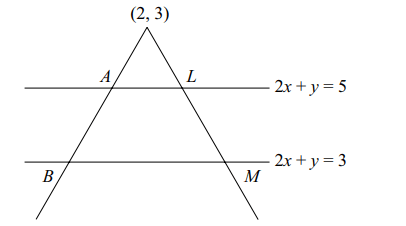
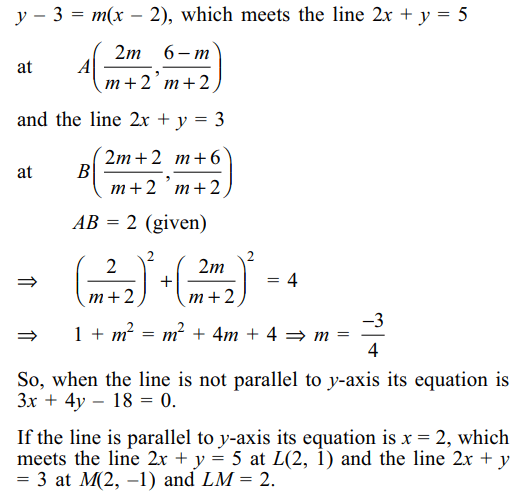
7. A line through the point (a, 0) meets the
curve \[y^{2}=4ax \] at \[P\left(x_{1},y_{1}\right)\] and \[Q\left(x_{2},y_{2}\right)\] then
a) \[x_{1}x_{2}=a^{2}\]
b) \[x_{1}x_{2}-y_{1}y_{2}=5a^{2}\]
c) \[y_{1}y_{2}=-4a^{2}\]
d) All of the Above
Explanation: Let the equation of the line through (a, 0) be y = m(x – a), which meets the curve y2= 4ax at points for which m2(x – a)2 = 4ax
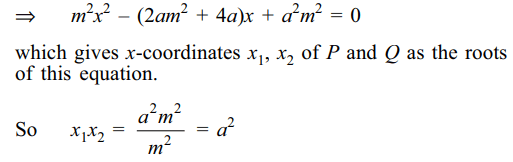
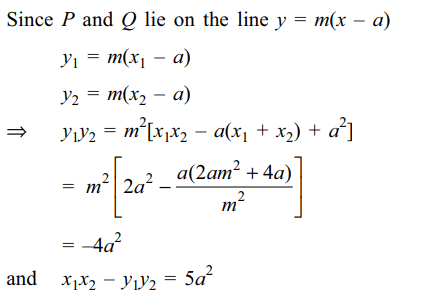
8. If the two lines represented by
\[x^{2}\left(\tan^{2} \theta+\cos^{2}\theta\right)-2xy \tan\theta+y^{2}\sin^{2}\theta=0\]
make angles
\[\alpha,\beta\] with the x-axis, then
a) \[\tan\alpha+\tan\beta=4cosec2\theta\]
b) \[\frac{\tan\alpha}{\tan\beta}=\frac{2+\sin2\theta}{2-\sin2\theta}\]
c) \[\tan\alpha-\tan\beta=2\]
d) All of the Above
Explanation: Let the lines represented by the given equation be


9. If two of the lines given by \[3x^3+3x^2y-3xy^2+dy^3=0\] are at right angles then the slope of one of
them is
a) -1
b) 1
c) 3
d) Both a and b
Explanation: Let the lines represented by the given equations

10. \[9x^2+2hxy+4y^2+6x+2fy-3=0\] represent two parallel lines if
a) h = 6, f = 2
b) h = -6, f = -2
c) h = -6, f = 2
d) Both a and b
Explanation: Since the given equation represents a pair of parallel lines, we have
