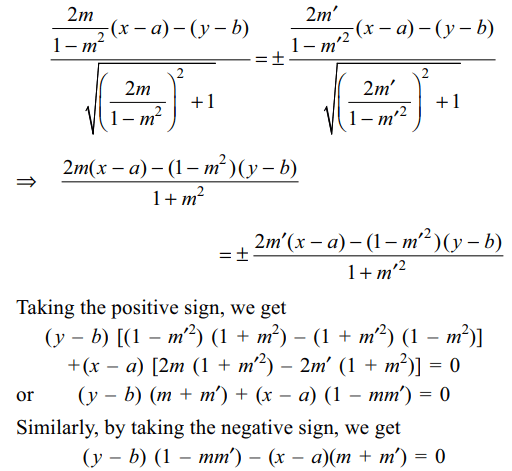1. The equation x – y = 4 and x2 + 4xy + y2
= 0 represent the sides of
a) an equilateral triangle
b) a right angled triangle
c) an isosceles triangle
d) none of these
Explanation:

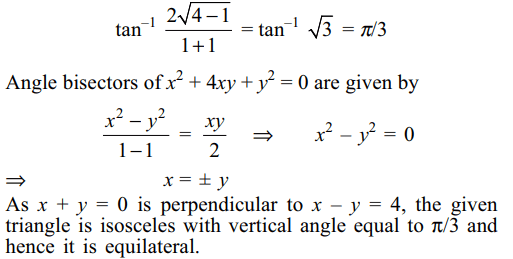
2. If the equation of the pair of straight lines
passing through the point (1, 1), one making an angle \[\theta\]
with the positive direction of x-axis and the other making
the same angle with the positive direction of y-axis is
\[x^{2}-\left(a+2\right)xy+y^{2}+a\left(x+y-1\right)=0 ,a\neq -2\]
then the
value of sin \[2\theta\] is
a) a – 2
b) a + 2
c) 2/(a + 2)
d) 2/a
Explanation: Equations of the given lines are

3. If \[\theta_{1}\] and \[\theta_{2}\] be the angles which the lines
\[\left(x^{2}+y^{2}\right)\left(\cos ^{2}\theta\sin^{2}\alpha+\sin^{2}\theta\right)=\left(x\tan\alpha-y\sin\theta\right)^{2}\]
make
with the axis of x, then if \[\theta=\pi/6 ,\tan\theta_{1} +\tan\theta_{2}\] is equal to
a) \[\left(-8/3\right)\sin^{2}\alpha\]
b) (-8/3)cosec 2 \[\alpha\]
c) -8 cosec 2 \[\alpha\]
d) -4 cosec 2 \[\alpha\]
Explanation: The given equation can be written as

4.If two of the lines represented by
\[x^{4}+x^{3}y+cx^{2}y^{2}-xy^{3}+y^{4}=0\]
bisect the angle between the other two, then the value of
c is
a) 0
b) -1
c) 1
d) -6
Explanation: Since the product of the slopes of the four lines represented by the given equation is 1 and a pair of lines represent the bisectors of the angles between the other two, the product of the slopes of each pair is –1. So let the equation of one pair be
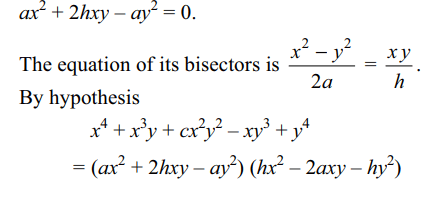
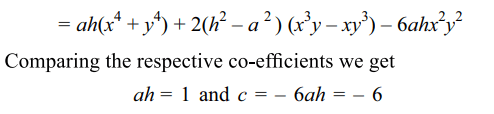
5. The coordinates of a point at unit distance
from the lines 3x – 4y + 1 = 0 and 8x + 6y + 1
= 0 are
a) \[\left(\frac{6}{5},\frac{-1}{10}\right)\]
b) \[\left(0,\frac{3}{2}\right)\]
c) \[\left(\frac{-2}{5},\frac{-13}{10}\right)\]
d) All of the Above
Explanation: Coordinates (x, y) of the required point are given by

6. Equations (b – c)x + (c – a)y + (a – b) = 0
and \[\left(b^3 – c^3\right)x +\left(c^3 – a^3\right)y + a^3 – b^3 = 0\]
will represent the same line if
a) b = c
b) c = a
c) a = b
d) All of the Above
Explanation: The two lines will be identical if there exists some real number k, such that
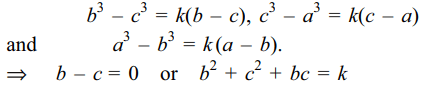
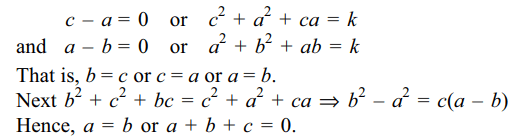
7. A rectangle ABCD has its side AB parallel
to the line y = 2x and vertices A, B and D on lines
y = 1, x = 1 and x = –1 respectively. The coordinates of
C can be
a) (3, 8)
b) (–3, 8)
c) (–3, –1)
d) Both a and c
Explanation:


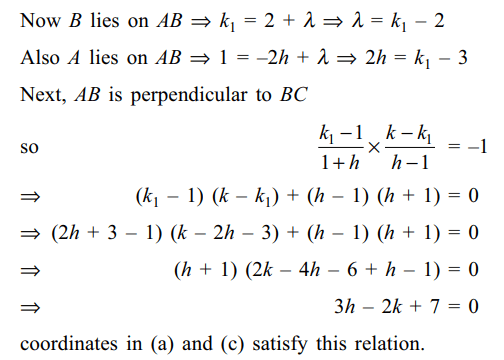
8. Equation of a straight line passing through
the point (4, 5) and equally inclined to the lines
3x = 4y + 7 and 5y = 12x + 6 is
a) 9x – 7y = 1
b) 9x + 7y = 71
c) 7x + 9y = 73
d) Both a and c
Explanation: The required lines are parallel to the angle bisectors of the given lines. The angle bisectors of the given lines are
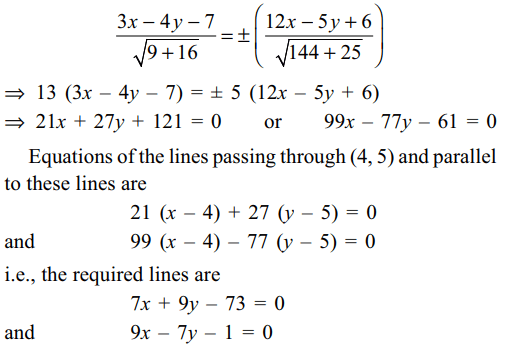
9. For all values of \[\theta\] , the lines represented
by the equation\[\left(2\cos\theta+3\sin\theta\right)x+\left(3\cos\theta-5\sin\theta\right)y-\left(5\cos\theta-2\sin\theta\right)=0\]
a) pass through a fixed point
b) pass through the point (1, 1)
c) pass through a fixed point whose reflection in the line \[x+y=\sqrt{2}\] is \[\left(\sqrt{2}-1,\sqrt{2}-1\right)\]
d) All of the Above
Explanation: The given equation can be written as

10. Equation of a bisector of the angle
between the lines
\[y-b=\frac{2m}{1-m^2}\left(x-a\right)\]
and \[y-b=\frac{2m'}{1-m'^2}\left(x-a\right)\]
a) (y - b) (m + m') + (x - a) (1 - mm') = 0
b) (y - b) (1 - mm') + (x - a) (m + m') = 0
c) (x - a) (m + m') - (y - b) (1 - mm') = 0
d) Both a and c
Explanation: Equations of the bisectors are given by