1. The relationship between coefficient of permeability and coefficient of percolation is ______
a) kp=kn
b) kp=ke
c) kp=k/e
d) kp=k/n
Explanation: From Darcy’s law, V=ki
And Vs=kpi
∴ Vs/V=kp/k=1/n
∴ kp=k/n.
2. If the coefficient of permeability of soil is 9*10-7cm/s and porosity is 0.33, then its coefficient of percolation is ______
a) 8*10-7cm/s
b) 27*10-7cm/s
c) 26*10-7cm/s
d) 13*10-7cm/s
Explanation: Given,
coefficient of permeability k=9*10-7cm/s
porosity n=0.33
coefficient of percolation kp=k/n=(9*10-7)/0.33
∴ kp=27*10-7cm/s.
3. If the coefficient of percolation is 18*10-7cm/s and void ratio is 0.5, then the coefficient of permeability k is _________
a) 26*10-7cm/s
b) 6*10-7 cm/s
c) 3*10-7cm/s
d) 13*10-7cm/s
Explanation: Given,
coefficient of percolation kp=18*10-7cm/s
void ratio e= 0.5
n=e/(1+e)=0.5/(1+0.5)=0.33
since kp=k/n
k= kp*n
k=(18*10-7)*0.33
k=6*10-7 cm/s.
4. For flow of water in tube, the velocity at surface is ___________
a) zero
b) equal to velocity at 1/3 of diameter
c) equal to velocity at 1/2 of diameter
d) equal to velocity at centre
Explanation: The surface of the tube is wet forming a very thin layer of water that is immobile due to molecular attraction. So the velocity at the surface is zero.
5. In Poiseuille’s law of flow, the variation of the velocity is given by _______
a) v = \(\frac{hγ_w}{4ηL}(r^2-R^2)\)
b) v = \(\frac{hγ_w}{14ηL}(R^2-r^2)\)
c) v = \(\frac{hγ_w}{4ηL}(R^2-r^2)\)
d) v = \(\frac{hγ_w}{8ηL}(R^2-r^2)\)
Explanation: Consider a capillary tube of length L and radius R.
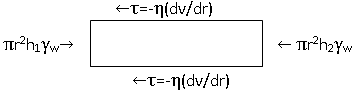
In equilibrium the sum of the forces is zero,
πr2h1γw– πr2h1γw-τ(2πrL)=0
on simplification, \(dv=-\frac{hγ_w}{2ηL}rdr\)
on integration,
\(v =- \frac{hγ_w}{4ηL}r^2 + C \,where\, C=\frac{hγ_w}{4ηL} R^2\)
∴ \(v = \frac{hγ_w}{4ηL}(R^2-r^2).\)
6. The velocity of flow of water at the centre of tube is _______ when the head is 0.1m, η=8.9*10-3 dynes-s/cm2, γw=1 g/cm3, the length is 10m and the diameter is 20cm
a) 20 cm/s
b) 22 cm/s
c) 28 cm/s
d) 30 cm/s
Explanation: given,
h=0.1m
η=8.9*10-3 dynes-s/cm2
γw=1 g/cm3
L= 10m
d= 20cm.
Since \(v = \frac{hγ_w}{4ηL}(R^2-r^2)\)
\(v = \frac{10*1}{4*8.9*10^{-3}*1000}(10^2-0^2)\)
v=28 cm/s.
7. The quantity of water flowing in thin cylindrical sheet of thickness dr is ____________
a) \(dq=\frac{hγ_w}{4ηL}(R^2-r^2)2πrdr\)
b) \(dq=\frac{hγ_w}{4ηL}(R^2-r^2)4πrdr\)
c) \(dq=\frac{hγ_w}{4ηL}(R^2-r^2)8πrdr\)
d) \(dq=\frac{hγ_w}{4ηL}(R^2-r^2)12πrdr\)
Explanation: Consider a capillary tube of length L and radius R.
dq=(2πrdr)v
substituting for velocity,
\(dq=(2πrdr)*\frac{hγ_w}{4ηL}(R^2-r^2)\)
\( ∴ dq=\frac{hγ_w}{4ηL}(R^2-r^2)2πrdr.\)
8. The total quantity of water flowing through the capillary tube is given by _________
a) \(q=\frac{hγ_w}{4ηL} R^2 \)
b) \(q=\frac{hγ_w}{4ηL} R^4\)
c) \(q=\frac{hγ_w}{8ηL} R^2\)
d) \(q=\frac{hγ_w}{8ηL} πR^4\)
Explanation: The total quantity of flow is obtained by integrating with the limits 0 to R in the differential discharge.
\(dq=\frac{hγ_w}{4ηL} (R^2-r^2)2πrdr\)
\(q=\frac{hγ_w}{4ηL}\int_0^R (R^2-r^2)2πrdr\)
\( ∴ q=\frac{hγ_w}{8ηL} πR^4\)
9. The total quantity of water with respect to the hydraulic gradient flowing through the capillary tube is given by _________
a) \( q=\frac{hiγ_w}{4ηL} R^2 \)
b) \( q=\frac{hγ_w}{4ηL} R^4/i\)
c) \( q=\frac{iγ_w}{8η} π R^2\)
d) \( q=\frac{iγ_w}{8η} πR^4\)
Explanation: The hydraulic gradient i is the head loss divided by the length travelled,
i=h/L
\( ∴ q=\frac{hγ_w}{8ηL} πR^4 = \frac{iγ_w}{8η}πR4.\)
10. The average velocity of the tube of area a is given by _________
a) \(v_{av}=\frac{iγ_w}{8ηπ}a \)
b) \(v_{av}=\frac{\frac{iγ_w}{8ηπ}}{a}\)
c) \(v_{av}=\frac{iγ_w}{2ηπ}a\)
d) \(v_{av}=\frac{\frac{iγ_w}{4ηπ}}{a}\)
Explanation: The average velocity is given by,
Vav=q/a
Vav=q/πr2
Substituting for q,
∴ \(v_{av}=\frac{iγ_w}{8ηπ}a. \)