PrepBharat

1. The adiabatic elasticity of a gas is equal to
a) \[\gamma\times density\]
b) \[\gamma\times volume\]
c) \[\gamma\times pressure\]
d) \[\gamma\times\]  specific heat

View Answer

2. The specific heat at constant pressure and at constant volume for an ideal gas are \[C_{p}\] and \[C_{v}\] and its adiabatic and isothermal elasticities are \[E_{\phi}\] and \[E_{\theta}\] respectively. The ratio of \[E_{\phi}\] to \[E_{\theta}\]
a) \[C_{v}\diagup C_{p}\]
b) \[C_{p}\diagup C_{v}\]
c) \[C_{p} C_{v}\]
d) \[1\diagup C_{p} C_{v}\]

View Answer

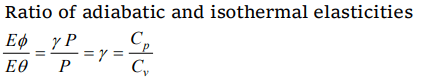
3. The only elastic modulus that applies to fluids is
a) Young's modulus
b) Shear modulus
c) Modulus of rigidity
d) Bulk modulus

View Answer

4. The ratio of the adiabatic to isothermal elasticities of a triatomic gas is
a) 3/4
b) 4/3
c) 1
d) 5/3

View Answer

5. If the volume of the given mass of a gas is increased four times, the temperature is raised from 27°C to 127°C. The elasticity will become
a) 4 times
b) 1/4 times
c) 3 times
d) 1/3 times

View Answer

6. If a rubber ball is taken at the depth of 200 m in a pool, its volume decreases by 0.1%. If the density of the water is \[1\times 10^{3}kg\diagup m^{3}\]  and \[g= 10 m\diagup s^{2}\]  , then the volume elasticity in \[ N\diagup m^{2}\] will be
a) \[ 10^{8}\]
b) \[ 2\times10^{8}\]
c) \[ 10^{9}\]
d) \[ 2\times10^{9}\]

View Answer

7.The compressibility of a material is
a) Product of volume and its pressure
b) The change in pressure per unit change in volume strain
c) The fractional change in volume per unit change in pressure
d) None of the above

View Answer

8. When a pressure of 100 atmosphere is applied on a spherical ball, then its volume reduces to 0.01%. The bulk modulus of the material of the rubber in \[dyne\diagup cm^{2}\]  is
a) \[ 10\times10^{12}\]
b) \[ 100\times10^{12}\]
c) \[ 1\times10^{12}\]
d) \[ 20\times10^{12}\]

View Answer

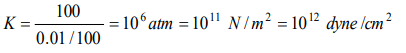
9. In the three states of matter, the elastic coefficient can be
a) Young's modulus
b) Coefficient of volume elasticity
c) Modulus of rigidity
d) Poisson's ratio

View Answer

10. Bulk modulus was first defined by
a) Young
b) Bulk
c) Maxwell
d) None of the above

View Answer