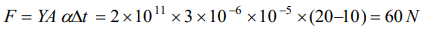1.A steel ring of radius r and cross-section area ‘A’ is fitted on to a wooden disc of radius \[R\left(R>r\right)\] . If Young's modulus be E, then the force with which
the steel ring is expanded is
a) \[AE\frac{R}{r}\]
b) \[AE\left(\frac{R-r}{r}\right)\]
c) \[\frac{E}{A}\left(\frac{R-r}{A}\right)\]
d) \[\frac{Er}{AR}\]
Explanation:

2. A wire extends by 1 mm when a force is applied. Double the force is applied to another wire of same material and length but half the radius of
cross-section. The elongation of the wire in mm will be
a) 8
b) 4
c) 2
d) 1
Explanation:
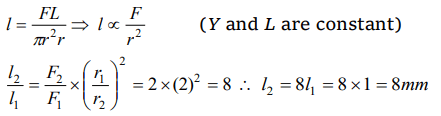
3.Two wires of the same material have lengths in the ratio 1 : 2 and their radii are in the ratio \[1:\sqrt{2}\] . If they are stretched by applying equal
forces, the increase in their lengths will be in the ratio
a) \[2:\sqrt{2}\]
b) \[\sqrt{2}:2\]
c) 1 : 1
d) 1 : 2
Explanation:
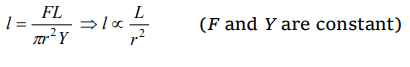
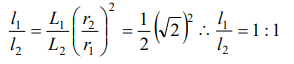
4. When a weight of 10 kg is suspended from a copper wire of length 3 metres and diameter 0.4 mm, its length increases by 2.4 cm. If the
diameter of the wire is doubled, then the extension in its length will be
a) 9.6 cm
b) 4.8 cm
c) 1.2 cm
d) 0.6 cm
Explanation:
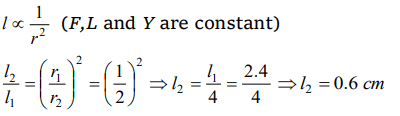
5. A force of \[ 10^{3}\] newton stretches the length of a hanging wire by 1 millimetre. The force required
to stretch a wire of same material and length but having four times the diameter by 1 millimetre is
a) \[4\times10^{3} N\]
b) \[16\times10^{3} N\]
c) \[\frac{1}{4}\times10^{3} N\]
d) \[\frac{1}{16}\times10^{3} N\]
Explanation:
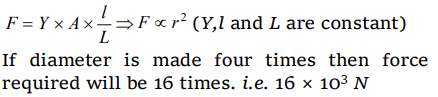
6. Density of rubber is d. A thick rubber cord of length L and cross-section area A undergoes elongation under its own weight on suspending it.
This elongation is proportional to
a) dL
b) Ad/L
c) \[Ad/L^{2} \]
d) \[dL^{2} \]
Explanation:

7. The ratio of two specific heats of gas Cp/Cv for argon is 1.6 and for hydrogen is 1.4. Adiabatic elasticity of argon at pressure P is E. Adiabatic elasticity of hydrogen will also be equal to E at
the pressure
a) P
b) \[\frac{8}{7}P\]
c) \[\frac{7}{8}P\]
d) 1.4 P
Explanation:
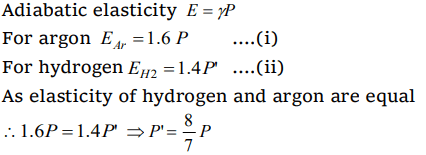
8. The relation between \[\gamma\] , \[\eta\] and K for a elastic material is
a) \[\frac{1}{\eta}=\frac{1}{3\gamma}+\frac{1}{9k}\]
b) \[\frac{1}{K}=\frac{1}{3\gamma}+\frac{1}{9\eta}\]
c) \[\frac{1}{\gamma}=\frac{1}{3K}+\frac{1}{9\eta}\]
d) \[\frac{1}{\gamma}=\frac{1}{3\eta}+\frac{1}{9K}\]
Explanation: \[\frac{1}{\gamma}=\frac{1}{3\eta}+\frac{1}{9K}\]
9.A fixed volume of iron is drawn into a wire of length L. The extension x produced in this wire by
a constant force F is proportional to
a) \[\frac{1}{L^{2}}\]
b) \[\frac{1}{L}\]
c) \[L^{2}\]
d) L
Explanation:
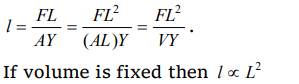
10. A wire of cross-sectional area 3 mm2 is first stretched between two fixed points at a temperature of 20°C. Determine the tension when
the temperature falls to 10°C. Coefficient of linear expansion \[ \alpha=10^{-5\circ}C^{-1}\] and \[ Y=2\times10^{11} N\diagup m^{2}\]
a) 20 N
b) 30 N
c) 60 N
d) 120 N
Explanation: