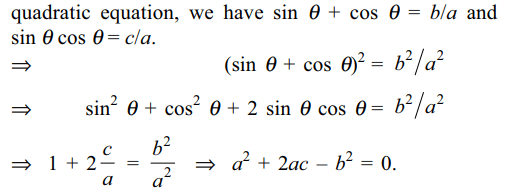1. If \[3\sin \theta+4\cos \theta=5\] , then the value of
\[4\sin \theta-3\cos \theta\] is equal to
a) 3
b) 2
c) 1
d) 0
Explanation:
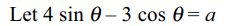
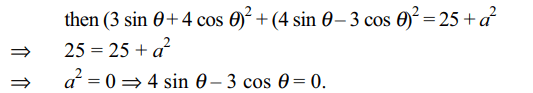
2. \[\sin^{2}12^{\circ}+\sin^{2}21^{\circ}+\sin^{2}39^{\circ}+\sin^{2}48^{\circ}-\sin^{2}9^{\circ}-\sin^{2}18^{\circ}\]
is equal to
a) -1
b) 0
c) 1/2
d) 1
Explanation:
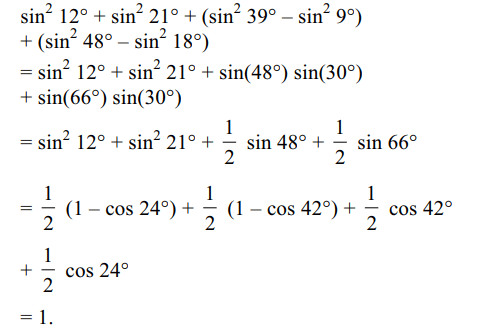
3. \[ \cos 2\alpha-2\sin^{2}\beta-4\cos \left(\alpha+\beta\right)\sin\alpha\sin\beta-\cos 2\left(\alpha+\beta\right)\]
is independent of
a) \[\alpha\]
b) \[\beta\]
c) both \[\alpha\] and \[\beta\]
d) none of these
Explanation:
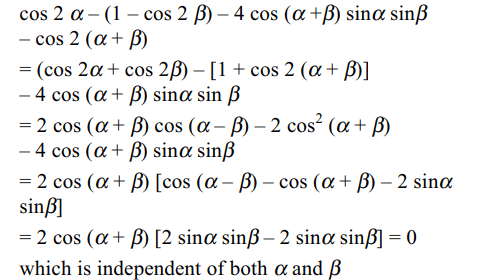
4. If \[\frac{\sin\theta}{\cos3\theta}+\frac{\sin3\theta}{\cos9\theta}+\frac{\sin9\theta}{\cos27\theta}=\frac{1}{2}\left(\tan x- \tan \theta\right)\]
then the value of x is
a) \[3\theta\]
b) \[6\theta\]
c) \[9\theta\]
d) \[27\theta\]
Explanation:
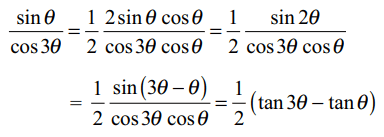
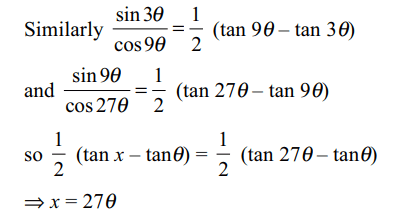
5. If \[2\sin \alpha\cos\beta\sin\gamma=\sin\beta\sin\left(\alpha+\gamma\right)\]
then \[\tan\alpha,\tan\beta,\tan\gamma\] are in
a) Arithmetic progression
b) Geometric progression
c) Harmonic progression
d) none of these
Explanation:
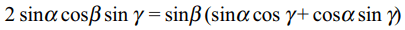
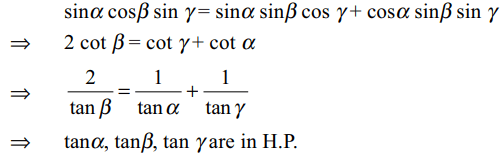
6. If \[\cot\alpha+\tan\alpha=m\] and \[\frac{1}{\cos\alpha}-\cos\alpha=n\] , then
a) \[m\left(mn^{2}\right)^{1/3}-n\left(nm^{2}\right)^{1/3}=1\]
b) \[m\left(m^{2}n\right)^{1/3}-n\left(mn^{2}\right)^{1/3}=1\]
c) \[n\left(mn^{2}\right)^{1/3}-m\left(nm^{2}\right)^{1/3}=1\]
d) \[n\left(m^{2}n\right)^{1/3}-m\left(mn^{2}\right)^{1/3}=1\]
Explanation:
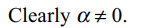
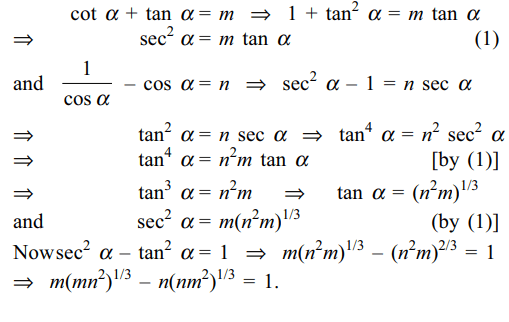
7. If \[a \cos ^{3}\alpha+3a\cos \alpha\sin^{2}\alpha =m\]
and \[a \sin ^{3}\alpha+3a\cos^{2} \alpha\sin\alpha =n\] , then \[\left(m+n\right)^{2/3}+\left(m-n\right)^{2/3}\] is equal to
a) \[2a^{2}\]
b) \[2a^{1/3}\]
c) \[2a^{2/3}\]
d) \[2a^{3}\]
Explanation: From the given relations, we get
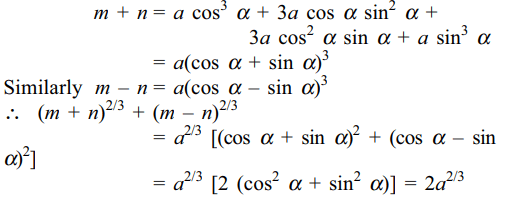
8. if \[\frac{2 \sin \alpha}{1+\cos\alpha+\sin\alpha}=y\] , then
\[\frac{1-\cos\alpha+\sin\alpha}{1+ \sin \alpha}\] is equal to
a) 1/y
b) y
c) 1-y
d) 1+y
Explanation:
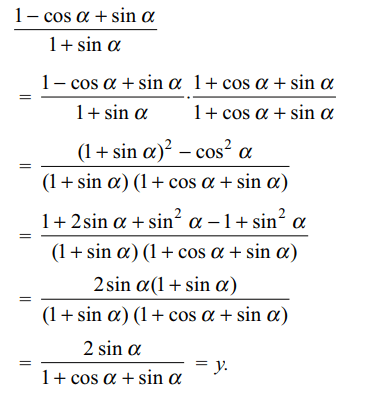
9. Minimum value of \[4x^{2}-4x \mid \sin\theta\mid -\cos^{2}\theta\]
is equal to
a) -2
b) -1
c) -1/2
d) 0
Explanation:
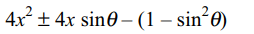
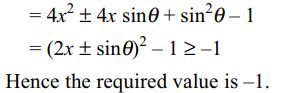
10. If \[\sin\theta\] and \[\cos\theta\] are the roots of the
equation \[ax^{2}-bx +c=0\] , then a, b and c satisfy the relation
a) \[a^{2}+b^{2}+2ac=0\]
b) \[a^{2}-b^{2}+2ac=0\]
c) \[a^{2}+c^{2}+2ab=0\]
d) \[a^{2}-b^{2}-2ac=0\]
Explanation: Since sin \[\theta\] and cos \[\theta\] are roots of the given