1. \[\left(\sin\alpha+ cosec\alpha\right)^{2}+\left(\cos\alpha+\sec\alpha\right)^{2}-\left(\tan^{2}\alpha+\cot ^{2}\alpha\right)\]
for all values of \[\alpha\] is equal to
a) 0
b) 2
c) 4
d) 7
Explanation:
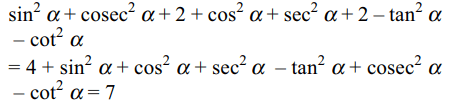
2. The expression
\[3\left[\sin^{4}\left(\frac{3\pi}{2}-\alpha\right)+\sin^{4}\left(3\pi+\alpha\right)\right]-2\left[\sin^{6}\left(\frac{\pi}{2}+\alpha\right)+\sin^{6}\left(5\pi-\alpha\right)\right]\]
is equal to
a) 0
b) -1
c) 1
d) 3
Explanation:
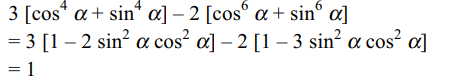
3. If \[\sin\left(x+3\alpha\right)=3\sin\left(\alpha-x\right)\] , then
a) \[\tan x = \tan\alpha\]
b) \[\tan x = \tan^{2}\alpha\]
c) \[\tan x = \tan^{3}\alpha\]
d) \[\tan x =3 \tan\alpha\]
Explanation:

4. If \[\frac{\cos \left(\theta-\alpha\right)}{\sin\left(\theta+\alpha\right)}=\frac{m+1}{m-1}\]
then m is equal to
a) \[\tan\left(\frac{\pi}{4}-\theta\right)\tan\left(\frac{\pi}{4}-\alpha\right)\]
b) \[\tan\left(\frac{\pi}{4}-\theta\right)\tan\left(\frac{\pi}{4}+\alpha\right)\]
c) \[\tan\left(\frac{\pi}{4}+\theta\right)\tan\left(\frac{\pi}{4}+\alpha\right)\]
d) \[\tan\left(\frac{\pi}{4}+\theta\right)\tan\left(\frac{\pi}{4}-\alpha\right)\]
Explanation:

5. The value of tan 130° tan 140° is equal to
a) -1
b) 1
c) \[1/\sqrt{3}\]
d) \[1+\sqrt{3}\]
Explanation:

6. If cos 1° cos 2° cos 3° ..... cos 179° = x + 1, then x
is equal to
a) -1
b) 0
c) 1
d) none of these
Explanation:

7. If \[-\pi/4\leq x<\pi/4\] and
\[\frac{1+\tan x}{1-\tan x} =1+\sin 2x\]
then tan x is equal to
a) -1
b) \[-1/\sqrt{3}\]
c) 1
d) 2
Explanation:
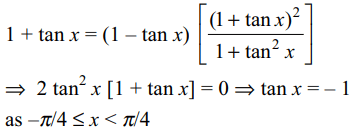
8. If \[\tan\alpha =\frac{m}{m-1}\] and \[\tan\beta =\frac{1}{2m-1}\] then
a) \[\alpha+\beta =\pi/4\]
b) \[\alpha-\beta =\pi/4\]
c) \[\alpha+\beta =\pi/6\]
d) \[\alpha-\beta =\pi/3\]
Explanation:
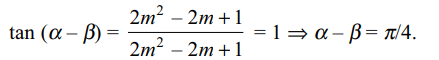
9. If \[ m \tan\left(\theta-30^{\circ}\right)=n \tan\left(\theta+120^{\circ}\right)\]
then
\[\frac{m-n}{m+n}\] is equal to
a) \[2 \cos 2\theta\]
b) \[2 \sin^{2}\theta\]
c) \[1/\left(2 \cos 2\theta\right)\]
d) \[1/\left(2 \sin 2\theta\right)\]
Explanation:

10. If \[\cos x+\sin x=\sqrt{2} \cos x\] , then \[\tan ^{2}x+2\tan x\]
is
equal to
a) 0
b) 1
c) 2
d) 3
Explanation:
