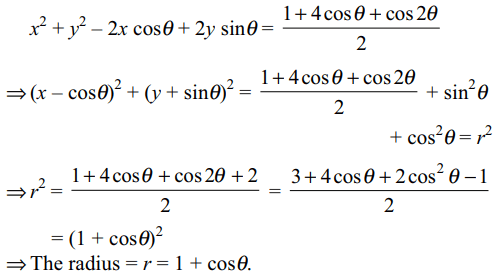1.If \[\sin x+\sin^{2}x=1\] then the value of
\[\cos^{12} x+3\cos^{10} x+3\cos^{8} x+\cos^{6} x-1\]
is equal to
a) 0
b) 1
c) -1
d) 2
Explanation:

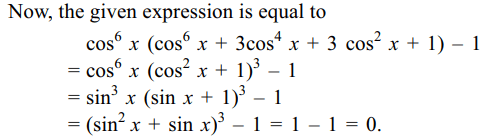
2. If \[\theta\] lies in the first quadarnt and
\[\cos \theta=8/17\] , then the value of \[\cos\left(30^{\circ}+\theta\right)+\cos\left(45^{\circ}-\theta\right)+\cos\left(120^{\circ}-\theta\right)\]
a) \[\left(\frac{\sqrt{3}-1}{2}+\frac{1}{\sqrt{2}}\right)\frac{23}{17}\]
b) \[\left(\frac{\sqrt{3}+1}{2}+\frac{1}{\sqrt{2}}\right)\frac{23}{17}\]
c) \[\left(\frac{\sqrt{3}-1}{2}-\frac{1}{\sqrt{2}}\right)\frac{23}{17}\]
d) \[\left(\frac{\sqrt{3}+1}{2}-\frac{1}{\sqrt{2}}\right)\frac{23}{17}\]
Explanation:
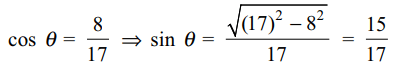
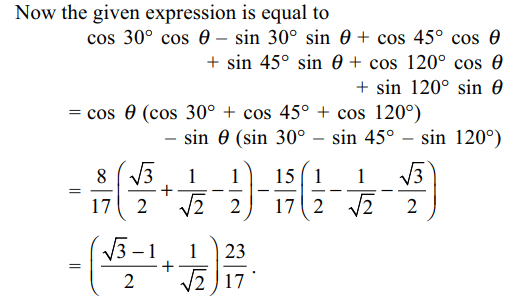
3. Let\[-\frac{\pi}{6}<\theta < - \frac{-\pi}{12}\] . Suppose
\[\alpha_{1}\] and \[\beta_{1}\] are the roots of the equation \[x^{2}-2x\sec\theta+1=0\] and
\[\alpha_{2}\] and \[\beta_{2}\] are the roots of the equation \[x^{2}+2x\tan\theta-1=0\] .
If \[\alpha_{1}> \beta_{1}\] and \[\alpha_{2}> \beta_{2}\] , then \[\alpha_{1}+ \beta_{2}\] equals
a) \[2\left(\sec\theta-\tan\theta\right)\]
b) \[2\sec\theta\]
c) \[-2\tan\theta\]
d) 0
Explanation:

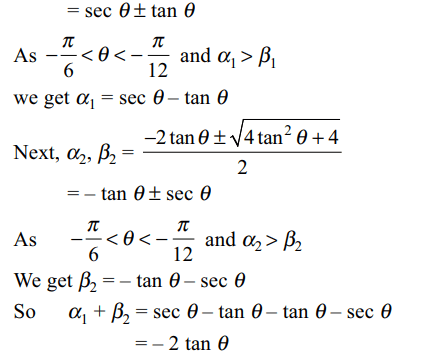
4. The value of the determinant \[\begin{bmatrix}1 & a & a^{2} \\\cos\left(n-1\right)x & \cos nx & \cos\left(n+1\right)x \\\sin\left(n-1\right)x & \sin nx & \sin\left(n+1\right)x\end{bmatrix}\]
(a \[\neq\] 1) is zero if
a) \[\sin x=0\]
b) \[\cos x=0\]
c) a=0
d) \[\cos x=\frac{1+a^{2}}{2a}\]
Explanation:
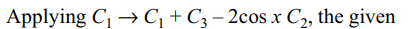
5. The value of \[\cos^{4}\left(\frac{\pi}{8}\right)+\cos^{4}\left(\frac{3\pi}{8}\right)+\cos^{4}\left(\frac{5\pi}{8}\right)+\cos^{4}\left(\frac{7\pi}{8}\right)\]
is equal to
a) 1/2
b) 3/4
c) 3/2
d) 1
Explanation:
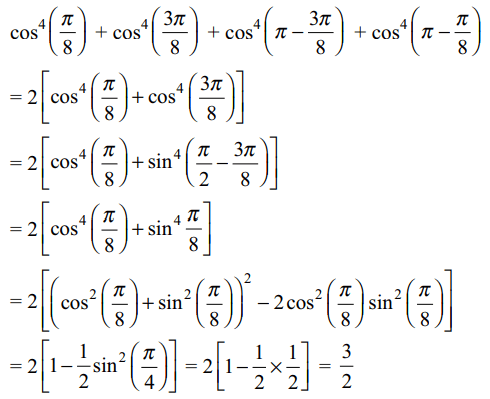
6. An angle \[\alpha\] is divided into two parts so
that the ratio of the tangents of these parts is \[\lambda\] . If the
difference between these parts is x then sin x/sin \[\alpha\] is equal
to
a) \[\gamma/\left(\gamma+1\right)\]
b) \[\left(\gamma-1\right)/\gamma\]
c) \[\frac{\gamma-1}{\gamma+1}\]
d) \[\frac{2\gamma}{\gamma+1}\]
Explanation:
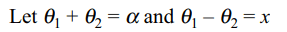

7. If \[\alpha\epsilon\left(0,\pi/2\right)\] , then the expression
\[\sqrt{x^{2}+x}+\frac{\tan^{2}x}{\sqrt{x^{2}+x}}\]
is always greater than or equal to
a) \[2\tan \alpha\]
b) 2
c) 1
d) \[\sec^{2} \alpha\]
Explanation: Since A.M ≥ G.M, we get
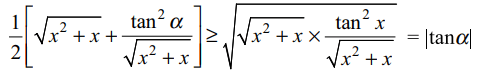
8. Given \[\theta\epsilon\left(0,\pi/4\right)\] and \[t_{1}=\left(\tan\theta\right)^{\tan\theta},t_{2}=\left(\tan\theta\right)^{\cot\theta},t_{3}=\left(\cot\theta\right)^{\tan\theta},t_{4}=\left(\cot\theta\right)^{\cot\theta}\]
then
a) \[t_{1}>t_{2}>t_{3}> t_{4}\]
b) \[t_{4}>t_{3}>t_{1}> t_{2}\]
c) \[t_{3}>t_{1}>t_{2}> t_{4}\]
d) \[t_{2}>t_{3}>t_{1}> t_{4}\]
Explanation:
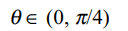
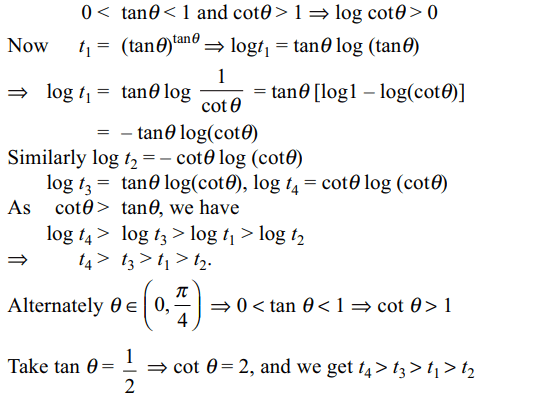
9. If \[x=\sin\alpha,y=\sin\beta,z=\sin\left(\alpha+\beta\right)\]
then
\[\cos\left(\alpha+\beta\right)\] =
a) \[\frac{x^{2}+y^{2}+z^{2}}{2xy}\]
b) \[\frac{x^{2}+y^{2}-z^{2}}{xy}\]
c) \[\frac{z^{2}-x^{2}-y^{2}}{2xy}\]
d) \[\frac{z^{2}-x^{2}-y^{2}}{xy}\]
Explanation:

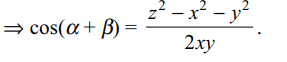
10. The radius of the circle
\[2x^{2}+2y^{2}-4x\cos\theta+4y\sin\theta-1-4\cos\theta-\cos2\theta=0\]
is
a) \[1-\cos\theta\]
b) \[1+\cos\theta\]
c) \[1-\sin\theta\]
d) none of these
Explanation: Equation of the circle can be written as