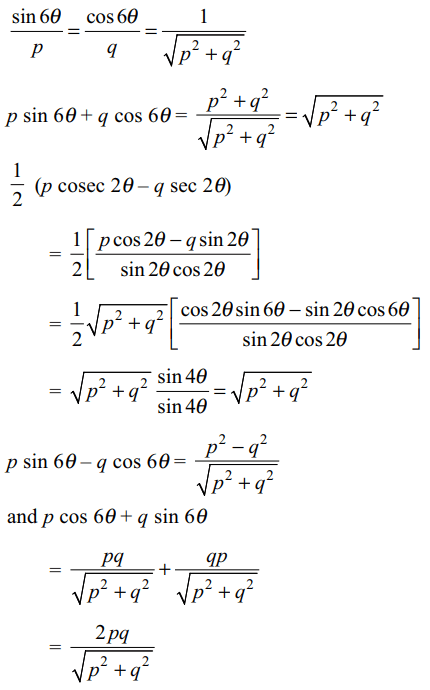1. If \[A=\sin ^{8}\theta+\cos ^{14}\theta\] , then for all values of \[\theta\]
a) A > 1
b) \[ A \geq 1\]
c) A < 1
d) \[ A \leq 1\]
Explanation:
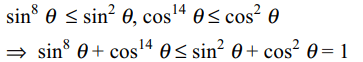
Note : A > 0 as A = 0 if sin \[\theta\] = cos \[\theta\] = 0 which is not possible.
2. If \[\pi/2< \alpha <\pi\] , then the expression
\[\sqrt{\frac{1-\sin\alpha}{1+\sin\alpha}}+\sqrt{\frac{1+\sin\alpha}{1-\sin\alpha}}\]
is equal to
a) \[2/\cos\alpha\]
b) \[-2/\cos\alpha\]
c) \[2/\sin\alpha\]
d) \[2\tan\alpha\]
Explanation:
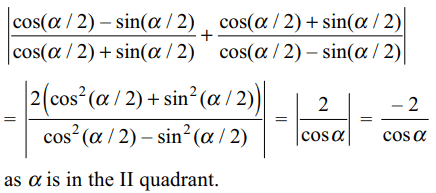
3. If \[0<\theta <\pi/2\] and \[\sin\theta+\cos\theta+\tan\theta+\cot\theta+\sec\theta+cosec\theta\]
is equal to 7, then sin 2\[\theta\] is a root
of the equation
a) \[x^{2}+44x+36=0\]
b) \[x^{2}-44x-36=0\]
c) \[x^{2}-44x+36=0\]
d) \[x^{2}+44x-36=0\]
Explanation:

4. If \[\frac{\cos\left(\theta_{1}-\theta_{2}\right)}{\cos\left(\theta_{1}+\theta_{2}\right)}+\frac{\cos\left(\theta_{3}+\theta_{4}\right)}{\cos\left(\theta_{3}-\theta_{4}\right)}=0\]
then \[\tan\theta_{1}\tan\theta_{2}\tan\theta_{3} \tan\theta_{4}\] is equal to
a) -1
b) 1
c) 2
d) 4
Explanation:

5. If \[\cos 2\beta=\frac{\cos\left(\alpha+\gamma\right)}{\cos\left(\alpha-\gamma\right)}\]
then \[\tan\alpha,\tan\beta\] and \[\tan\gamma\] are in
a) A.P
b) G.P
c) H.P
d) none of these
Explanation:

6. If \[x\cos \alpha+y \sin\alpha =x\cos\beta+y\sin\beta=2a\left(0<\alpha,\beta<\pi/2\right)\]
then
a) \[\cos \alpha+\cos\beta =\frac{4ax}{x^{2}+y^{2}}\]
b) \[\cos \alpha\cos\beta =\frac{4a^{2}-y^{2}}{x^{2}+y^{2}}\]
c) \[\sin \alpha+\sin\beta =\frac{4ay}{x^{2}+y^{2}}\]
d) All of the Above
Explanation:
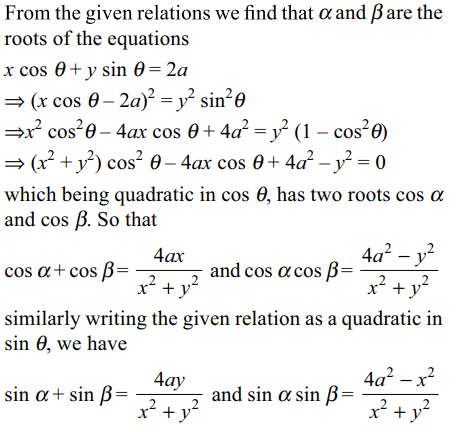
7. If \[y=\frac{\sqrt{1-\sin 4A}+1}{\sqrt{1+\sin4A}-1}\]
then one of the values of y is,
a) \[-\tan A\]
b) \[\cot A\]
c) \[\tan \left(\frac{\pi}{4}+A\right)\]
d) All of the Above
Explanation:
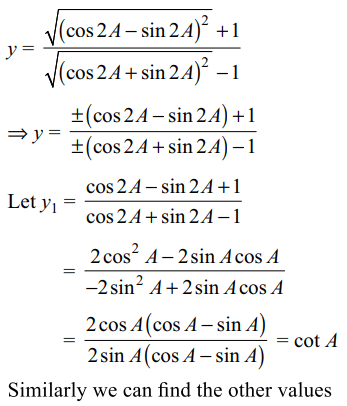
8. For \[0<\theta<\pi/2,\tan\theta+\tan2\theta+\tan 3\theta =0\] if
a) \[\tan\theta=0\]
b) \[\tan\theta\tan2\theta=2\]
c) \[\tan3\theta=0\]
d) Both b and c
Explanation:
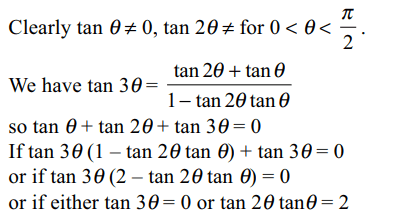
9. If \[\sin\theta\left(1+\sin\theta\right)+\cos\theta\left(1+\cos\theta\right)=x\]
and
\[\sin\theta\left(1-\sin\theta\right)+\cos\theta\left(1-\cos\theta\right)=y\]
then
a) \[x^{2}-2x=\sin2\theta\]
b) \[y^{2}+2y=\sin2\theta\]
c) \[xy=\sin2\theta\]
d) All of the Above
Explanation:

10. If \[\tan 6\theta=\frac{p}{q}\] , then
a) \[p\sin6\theta+q\cos6\theta=\sqrt{p^{2}+q^{2}}\]
b) \[\frac{1}{2}\] (p cosec \[2\theta-q\sec 2\theta)=\sqrt{p^{2}+q^{2}}\]
c) \[p\cos6\theta+q\sin6\theta=\frac{2pq}{\sqrt{p^{2}+q^{2}}}\]
d) All of the Above
Explanation: