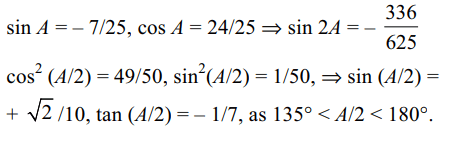1. \[\left(\frac{1+\sin\theta-\cos\theta}{1+\sin\theta+\cos\theta}\right)^{2}\] is equal to
a) \[\frac{1-\cos\theta}{1+\cos\theta}\]
b) \[\frac{1-\sin\theta}{1+\sin\theta}\]
c) \[\tan^{2}\frac{\theta}{2}\]
d) Both a and c
Explanation:
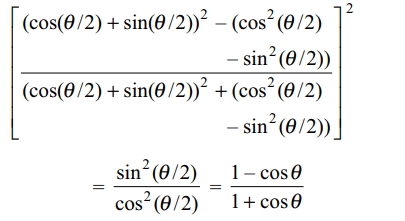
2. If \[\tan\theta =\frac{x^{2}+1}{x^{2}-1}\] ,then
a) \[\sin\theta =\frac{x^{2}+1}{\sqrt{2\left(x^{4}+1\right)}}\]
b) \[\sin\theta =\frac{x^{2}-1}{\sqrt{2\left(x^{4}+1\right)}}\]
c) \[\cos\theta =\frac{x^{2}-1}{\sqrt{2\left(x^{4}+1\right)}}\]
d) Both a and c
Explanation:

3. If \[\cot\theta +\tan\theta=x\] and \[\sec\theta -\cos\theta=y\] , then
a) \[\sin\theta \cos\theta=\frac{1}{x}\]
b) \[\sin\theta \tan\theta=y\]
c) \[\left(x^{2}y\right)^{2/3}-\left(xy^{2}\right)^{2/3}=1\]
d) All of the Above
Explanation:


4. If \[\cos\alpha=\frac{3}{5}\]
and \[\cos\beta=\frac{5}{13}\] ,then
a) \[\cos\left(\alpha-\beta\right)=\frac{63}{65}\]
b) \[\sin\left(\alpha+\beta\right)=\frac{56}{65}\]
c) \[\sin^{2}\frac{\alpha-\beta}{2}=\frac{1}{65}\]
d) All of the Above
Explanation:

5. The equation \[\sin^{6}x+\cos^{6}x=a^{2}\] has real solutions
if
a) \[a \epsilon\left(-1,1\right)\]
b) \[a \epsilon\left[-1,-\frac{1}{2}\right]\]
c) \[a \epsilon\left(-\frac{1}{2},\frac{1}{2}\right)\]
d) Both b and c
Explanation:
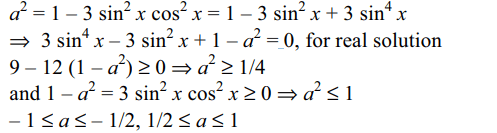
6. If \[\tan\alpha\] and \[\tan\beta\] are the roots of the equation
\[x^{2}+px+q=0\left(p\neq 0\right)\] , then
a) \[\sin^{2}\left(\alpha+\beta\right)+p \sin \left(\alpha+\beta\right)\cos\left(\alpha+\beta\right)+q\cos^{2}\left(\alpha+\beta\right)=q\]
b) \[\tan\left(\alpha+\beta\right)=\frac{p}{q-1}\]
c) \[\cos\left(\alpha+\beta\right)=1-q\]
d) Both a and b
Explanation:
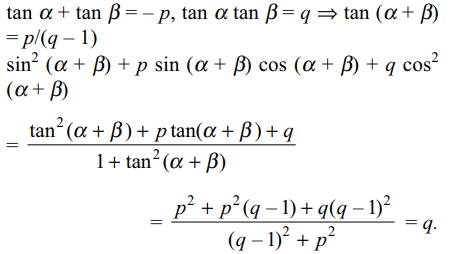
7. If \[\sin\theta+\sin\phi=a \] and \[\cos\theta+\cos\phi=b \] , then
a) \[\cos\frac{\theta-\phi}{2}=\pm\frac{1}{2}\sqrt{a^{2}+b^{2}}\]
b) \[\cos\left(\theta-\phi\right)=\frac{a^{2}+b^{2}-2}{2}\]
c) \[\tan\frac{\theta-\phi}{2}=\pm\sqrt{\frac{4-a^{2}-b^{2}}{a^{2}+b^{2}}}\]
d) All of the Above
Explanation:

8.If \[\tan\theta=\frac{\sin\alpha-\cos\alpha}{\sin\alpha+\cos\alpha}\] , then
a) \[\sin\alpha-\cos\alpha=\pm\sqrt{2}\sin\theta\]
b) \[\sin\alpha+\cos\alpha=\pm\sqrt{2}\cos\theta\]
c) \[\cos2\theta=\sin2\alpha\]
d) All of the Above
Explanation:
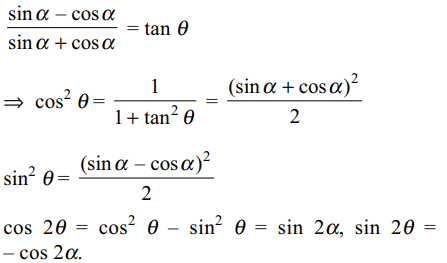
9. Which of the following statements are possible; a,
b, m and n being non-zero real numbers?
a) \[4\sin^{2}\theta =5\]
b) \[\left(a^{2}+b^{2}\right)\cos\theta=2ab\]
c) \[\left(m^{2}+n^{2}\right) cosec\theta=m^{2}-n^{2}\]
d) \[\sin \theta =2.375\]
Explanation:
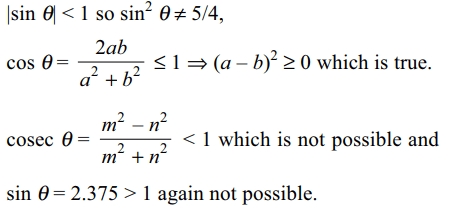
10. If A lies between 270° and 360° and sin A =
–7/25, then
a) \[\sin 2A=-\frac{336}{625}\]
b) \[\cos \frac{A}{2}=\frac{\sqrt{2}}{5}\]
c) \[\tan \frac{A}{2}=-\frac{1}{7}\]
d) Both a and c
Explanation: