1. Out of the following, the only pair that does not have identical dimensions is
a) Angular momentum and Planck's constant
b) Moment of inertia and moment of a force
c) Work and torque
d) Impulse and momentum
Explanation:
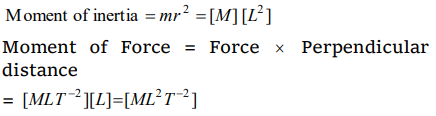
2. The dimensional formula for impulse is same as the dimensional formula for
a) Momentum
b) Force
c) Rate of change of momentum
d) Torque
Explanation: Momentum = mv = [MLT-1]
Impulse = Force * Time = [MLT-2] * [T] = [MLT-1]
3. Which of the following is dimensionally correct
a) Pressure = Energy per unit area
b) Pressure = Energy per unit volume
c) Pressure = Force per unit volume
d) Pressure = Momentum per unit volume per unit time
Explanation:
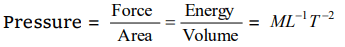
4. Planck's constant has the dimensions (unit) of
a) Energy
b) Linear momentum
c) Work
d) Angular momentum
Explanation: [h] = [Angular momentum] = [ML2T-1]
5. The equation of state of some gases can be expressed as \[\left(P+\frac{a}{V^{2}}\right)\left(V-b\right)=RT\] . Here P is the pressure, V is the volume, T is the absolute
temperature and a,b,R are constants. The dimensions of 'a' are
a) \[ML^{5}T^{-2}\]
b) \[ML^{-1}T^{-2}\]
c) \[M^{0}L^{3}T^{0}\]
d) \[M^{0}L^{6}T^{0}\]
Explanation: By principle of dimensional homogenity
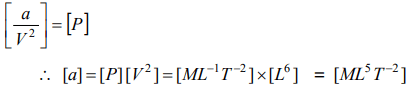
6. If V denotes the potential difference across the plates of a capacitor of capacitance C , the dimensions of \[CV^{2}\] are
a) Not expressible in MLT
b) \[MLT^{-2}\]
c) \[M^{2}LT^{-1}\]
d) \[ML^{2}T^{-2}\]
Explanation: \[\frac{1}{2}\] CV2 = Stored energy in a capacitor = [ML2T-2]
7. If L denotes the inductance of an inductor through which a current i is flowing, the dimensions of \[Li^{2}\] are
a) \[ML^{2}T^{-2}\]
b) Not expressible in MLT
c) \[MLT^{-2}\]
d) \[M^{2}L^{2}T^{-2}\]
Explanation: \[\frac{1}{2}\] Li2 = Stored energy in an inductor = [ML2T-2]
8. Of the following quantities, which one has dimensions different from the remaining three
a) Energy per unit volume
b) Force per unit area
c) Product of voltage and charge per unit volume
d) Angular momentum per unit mass
Explanation:
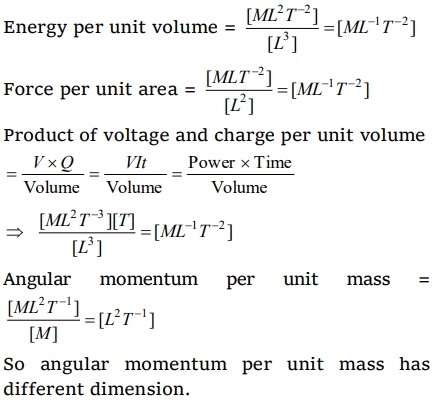
9. A spherical body of mass m and radius r is allowed to fall in a medium of viscosity \[\eta\]. The time in which the velocity of the body increases from zero to 0.63 times the terminal velocity (v)
is called time constant \[\left(\tau\right)\] . Dimensionally \[\tau\] can be represented by
a) \[\frac{mr^{2}}{6\pi\eta}\]
b) \[\sqrt{\left(\frac{6\pi mr \eta}{g^{2}}\right)}\]
c) \[\frac{m}{6\pi\eta rv}\]
d) None of the above
Explanation: Time constant \[\tau\] = [T] and Viscosity \[\eta\] = [ML-1T-1]. For options (a), (b) and (c) dimensions are not matching with time constant.
10. The frequency of vibration f of a mass m suspended from a spring of spring constant K is given by a relation of this type \[f=Cm^{x}K^{y}\] ; where C is a dimensionless quantity. The value of x and y are
a) \[X=\frac{1}{2},Y=\frac{1}{2}\]
b) \[X=-\frac{1}{2},Y=-\frac{1}{2}\]
c) \[X=\frac{1}{2},Y=-\frac{1}{2}\]
d) \[X=-\frac{1}{2},Y=\frac{1}{2}\]
Explanation:
